题目内容
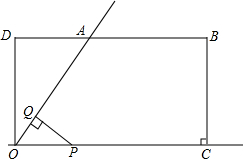 如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.(1)求S与t的函数关系式;
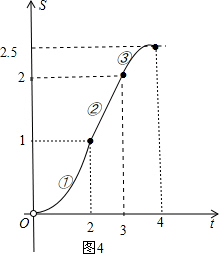
(2)画出S与t的函数图象.
考点:四边形综合题
专题:
分析:(1)分类讨论:作AE⊥OA交OC于E,如图1,先利用等腰直角三角形的性质计算出OA=
OD=
,OQ=
OP=
t,则OE=
OA=2,当点P在OE上运动时,即0<t≤2时,S=S△POQ,根据三角形面积公式得到=
t2;作CF⊥OA于F,PQ交AB于M,如图2,当点P在EC上运动时,即2<t≤3,S=S梯形AOPM,根据梯形的面积公式得到S=t-1;过B点作BH⊥OA于H,PQ交矩形的边于N、K,如图3,当点P在CW上运动时,即3<t<4,利用S=S梯形ABCO-S△BNK得到S=-
t2+4t-
;
(2)利用自变量的取值范围分别画出二个二次函数图象和一个一次函数图象.
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 11 |
| 2 |
(2)利用自变量的取值范围分别画出二个二次函数图象和一个一次函数图象.
解答:解:(1)作AE⊥OA交OC于E,如图1,
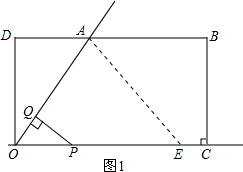
∵OA平分∠DOC,
∴∠AOD=∠AOC=45°,
∵PQ⊥OA,EA⊥OA
∴△ADO、△OPQ和△OEA都是直角三角形,
∴OA=
OD=
,OQ=
OP=
t,
∴OE=
OA=2,
∴当0<t≤2时,S=S△POQ=
•(
t)2=
t2;
作CF⊥OA于F,PQ交AB于M,如图2,
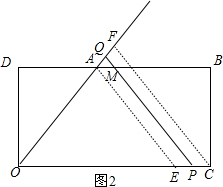
∵OQ=
t,
∴AQ=OQ-OA=OQ=
t-
,
∴AM=
AQ=
(
t-
)=t-2,
∴当2<t≤3时,S=S梯形AOPM=
×(t-2+t)×1=t-1;
过B点作BH⊥OA于H,PQ交矩形的边于N、K,如图3,
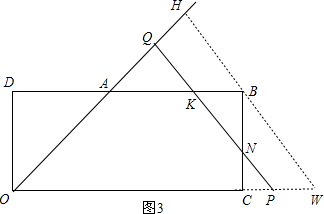
∵NC=PC=t-3,
∴BN=BC-NC=1-(t-3)=4-t,
∴当3<t<4时,S=S梯形ABCO-S△BNK
=
(2+3)×1-
(4-t)2
=-
t2+4t-
,
综上所述,S与t的函数关系式为
当0<t≤2时,S=
t2①;当2<t≤3时,S=t-1②;当3<t<4时,S=-
t2+4t-
③;
(2)如图4:
 :
:

∵OA平分∠DOC,
∴∠AOD=∠AOC=45°,
∵PQ⊥OA,EA⊥OA
∴△ADO、△OPQ和△OEA都是直角三角形,
∴OA=
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴OE=
| 2 |
∴当0<t≤2时,S=S△POQ=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
作CF⊥OA于F,PQ交AB于M,如图2,

∵OQ=
| ||
| 2 |
∴AQ=OQ-OA=OQ=
| ||
| 2 |
| 2 |
∴AM=
| 2 |
| 2 |
| ||
| 2 |
| 2 |
∴当2<t≤3时,S=S梯形AOPM=
| 1 |
| 2 |
过B点作BH⊥OA于H,PQ交矩形的边于N、K,如图3,

∵NC=PC=t-3,
∴BN=BC-NC=1-(t-3)=4-t,
∴当3<t<4时,S=S梯形ABCO-S△BNK
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 11 |
| 2 |
综上所述,S与t的函数关系式为
当0<t≤2时,S=
| 1 |
| 4 |
| 1 |
| 2 |
| 11 |
| 2 |
(2)如图4:
 :
:点评:本题考查了四边形的综合题:熟练掌握矩形、等腰三角形的性质;会计算三角形和梯形的面积;会画一次函数和二次函数的图象;能运用分类讨论的思想解决数学问题.

练习册系列答案
相关题目
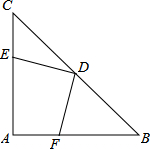 △ABC中,∠A=90°,AB=AC,D为BC中点,E、F分别在AC、AB上,且DE⊥DF,试判断DE、DF的数量关系,并说明理由.
△ABC中,∠A=90°,AB=AC,D为BC中点,E、F分别在AC、AB上,且DE⊥DF,试判断DE、DF的数量关系,并说明理由.