题目内容
小亮父亲想用长为80m栅栏,再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
(1)写出S与x的函数关系式,指出x的取值范围;
(2)当羊圈的长和宽分别为多少米时,羊圈的面积最大?最大面积是多少?
(1)写出S与x的函数关系式,指出x的取值范围;
(2)当羊圈的长和宽分别为多少米时,羊圈的面积最大?最大面积是多少?
考点:二次函数的应用
专题:
分析:(1)根据BC=(栅栏总长-2AB),再利用矩形面积公式即可求出;
(2)根据配方法法求出二次函数最值即可;
(2)根据配方法法求出二次函数最值即可;
解答:解:(1)∵AB=CD=xm,∴BC=(80-2x)m,
∴S=x(80-2x)=-2x2+80x,
∴
,
∴
,
∴
,
∴15≤x<40
∴S=-2x2+80x,(15≤x<40);
(2)∵S=-2(x2-40x+400-400)=-2(x-20)2+800,
∵15≤x<40,
∴当x=20时,S有最大值为800,
∴当x=20时,面积S有最大值为800;
∴S=x(80-2x)=-2x2+80x,
∴
|
∴
|
∴
|
∴15≤x<40
∴S=-2x2+80x,(15≤x<40);
(2)∵S=-2(x2-40x+400-400)=-2(x-20)2+800,
∵15≤x<40,
∴当x=20时,S有最大值为800,
∴当x=20时,面积S有最大值为800;
点评:本题考查了二次函数的应用,找到所给面积的等量关系是解决本题的关键;易错点是根据篱笆长得到矩形长的代数式.

练习册系列答案
相关题目
把分式
(a≠0,b≠0)的x,y都扩大到原来的10倍,则分式的值( )
| 2a2 |
| a-b |
| A、扩大到原来的10倍 | ||
B、缩小到原来的
| ||
| C、扩大到原来的100倍 | ||
| D、不变 |
一个轴对称图形某一点的对称点( )
| A、有且只有一个 | B、有两个 |
| C、可能有多个 | D、都不正确 |
抛物线y=-x2+1的对称轴是( )
| A、直线x=1 |
| B、直线x=0 |
| C、直线x=-1 |
| D、直线y=0 |

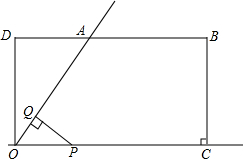 如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.