题目内容
将前300个正整数1,2,3,…,300顺次在黑板上排成一行,然后划去前两数1,2,而将这两数的和写在最后面,成为3,4,5,…,300,3;接着,再划去前两数3,4,又将这两数的和写在最后面,成为5,6,7,…,300,3,7;像这样一直进行下去,直到最后黑板上只剩下一个数为止;试求黑板上出现过的所有数之和(包括每次划去的数在内).
考点:整数问题的综合运用
专题:
分析:每次都是1+2+3+…+300,现在就是考虑要多少次完成:后面每一次都是每2个数的和,且都是比前一次加数的个数少一半,可得第一次完有300个数,第2次完150个数,第3次完75个数,但是第4次开始的时候,会用到下一次的数,但是不影响结果,所以第4次完后有38个数,第5次完有19个数,第6次完有10个数,第7次完有5个数,第8次完有3个,第9次完有2个,第10有1个数,根据每一次的和乘以次数,可得答案.
解答:解:根据题意,得1+2+3+…+300=
=45150,
后面每一次都是每2个数的和,且都是比前一次加数的个数少一半,每次的和相等,共出现10次,
黑板上出现过的所有数之和是
×10=451500,
答:黑板上出现过的所有数之和是451500.
| (1+300)×300 |
| 2 |
后面每一次都是每2个数的和,且都是比前一次加数的个数少一半,每次的和相等,共出现10次,
黑板上出现过的所有数之和是
| (1+300)×300 |
| 2 |
答:黑板上出现过的所有数之和是451500.
点评:本题考查了整数问题的综合运用,发现1+2+3+…+300出现的次数是解题关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
下列各式中,计算正确的是( )
| A、an•a2=a2n(n是整数) |
| B、(a2)3=a5 |
| C、a•a2•a3=a5 |
| D、a•(-a2)=-a3 |
笔尖在纸上快速滑动写出一个又一个字,用数学知识解释为( )
| A、点动成线 | B、线动成面 |
| C、面动成体 | D、以上答案都不对 |
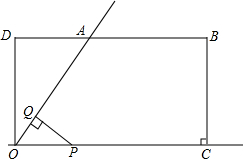 如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.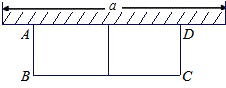 如图,有长为30米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米).设花圃的一边AB长为x米,面积为y平方米.
如图,有长为30米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米).设花圃的一边AB长为x米,面积为y平方米.