题目内容
边长为3的正方形纸片ABCD,将它绕正方形中心O逆时针旋转45°后到正方形A1B1C1D1的位置,则旋转前后两次重叠部分的多边形的周长为 .
考点:旋转的性质
专题:
分析:由正方形的性质和旋转的性质可知:旋转前后两次重叠部分的多边形是正八边形,所以可设AE=x,利用勾股定理可得EF=
x,又因为正方形的边长是3,所以可得x+
x+x=3,进而可求出EF的长,所以转前后两次重叠部分的多边形的周长可求出.
| 2 |
| 2 |
解答: 解:由正方形的性质和旋转的性质可知:旋转前后两次重叠部分的多边形是正八边形,
解:由正方形的性质和旋转的性质可知:旋转前后两次重叠部分的多边形是正八边形,
设AE=x,由勾股定理可得EF=
x,
又因为正方形的边长是3,
所以可得x+
x+x=3,
解得:x=3
-3,
所以旋转前后两次重叠部分的多边形的周长为8×(3
-3)=24
-24,
故答案为:24
-24.
 解:由正方形的性质和旋转的性质可知:旋转前后两次重叠部分的多边形是正八边形,
解:由正方形的性质和旋转的性质可知:旋转前后两次重叠部分的多边形是正八边形,设AE=x,由勾股定理可得EF=
| 2 |
又因为正方形的边长是3,
所以可得x+
| 2 |
解得:x=3
| 2 |
所以旋转前后两次重叠部分的多边形的周长为8×(3
| 2 |
| 2 |
故答案为:24
| 2 |
点评:本题考查了旋转的性质以及正方形的性质,解题的关键是由正方形的性质和旋转的性质可知:旋转前后两次重叠部分的多边形是正八边形.

练习册系列答案
相关题目
下列各式中不能用平方差公式计算的是( )
| A、(x-y)(x+y) |
| B、(-x-y)(-x+y) |
| C、(-x+y)(x+y) |
| D、(x-y)(y-x) |
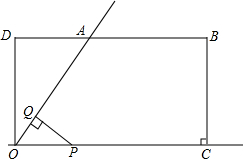 如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,在矩形OCBD中,OD=1,OC=3,∠DOC的角平分线交DB于A,动点P从O点出发,沿射线OC方向以每秒1个单位长度的速度移动,过点P作PQ⊥射线OA,垂足为Q,设点P移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.