题目内容
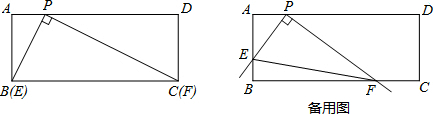
7. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①AD⊥EF;
②OA=OD;
③当∠A=90°时,四边形AEDF是正方形.
④AE2+DF2=AF2+DE2;
其中正确的是①③④.
分析 由AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,根据角平分线的性质,可得DE=DF,继而证得AE=AF,则可得AD是EF的垂直平分线;判定AD⊥EF;OA不一定等于OD;又由当∠A=90°时,可得四边形AEDF矩形,继而证得四边形AEDF是正方形;由AE=AF,DE=DF,即可判定AE2+DF2=AF2+DE2.
解答 解:∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,
∵∠ADE=90°-∠DAE,∠ADF=90°-∠DAF,
∴∠ADE=∠ADF,
∴AE=AF,
∴点A在EF的垂直平分线上,点D在EF的垂直平分线上,
∴AD是EF的垂直平分线,
即AD⊥EF;故①正确;
∵AD是EF的垂直平分线,
∴OE=OF,OA不一定等于OD;故②错误;
∵∠AED=∠EFD=90°,
∴当∠A=90°时,四边形AEDF是矩形,
∵DE=DF,
∴四边形AEDF是正方形;故③正确;
∵AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,∴④正确.
故答案为:①③④.
点评 此题是四边形综合题,考查了角平分线的性质、线段垂直平分线的性质、正方形的判定以及勾股定理等知识.注意证得AD是EF的垂直平分线是关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
18.在实数范围内,$\sqrt{x+1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≥-1 | C. | x≤1 | D. | x≤-1 |
11.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°,则∠NPB的度数是( )
| A. | 50° | B. | 60° | C. | 40°或140° | D. | 50°或130° |
14.下列长度的三条线段能组成三角形的是( )
| A. | 1、2、3 | B. | 3、3、7 | C. | 20、15、8 | D. | 5、15、8 |