��Ŀ����
17���ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1�������ǰ��ֱ�Ƕ�����ڵ�P�������ǰ����ֱ�DZ߷ֱ�����AB��BC���ཻ�ڵ�E��F������EF����1����ͼ������E���B�غ�ʱ����Fǡ�����C�غϣ����ʱPC�ij���
��2�������ǰ�ӣ�1���е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E���A�غ�ʱֹͣ������������У�����۲졢̽�������
�١�PEF�Ĵ�С�Ƿ����仯����˵�����ɣ�
������ת�У�����F��BC���е��غ�ʱ�����ı���AEFP�������
��ֱ��д���ӿ�ʼ��ֹͣ���߶�EF���е���������·�߳���
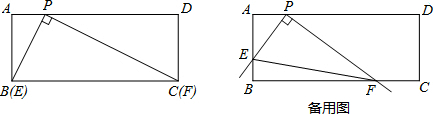
���� ��1��֤����ABP�ס�DPC���������������ε����ʵõ�$\frac{AP}{CD}$=$\frac{PB}{PC}$�����㼴�ɣ�
��2���ٹ���F��FG��AD�ڵ�G��֤����APE�ס�GFP���õ�$\frac{PF}{PE}$=$\frac{GF}{AP}$=2���������еĶ����ɣ�
����AE=x�����ݹ��ɶ����г�����x�ķ��̣��ⷽ�����x��ֵ���������ε������ʽ�������ε������ʽ���㣻
�۸����߶�EF���е����ʼλ�úͽ���λ�ý��
��� �⣺��1���ھ���ABCD�У���A=��D=90�㣬AP=1��CD=AB=2��
��PB=$\sqrt{5}$��
�ߡ�ABP+��APB=90�㣬��BPC=90�㣬
���ABP=��DPC��
���ABP�ס�DPC��
��$\frac{AP}{CD}$=$\frac{PB}{PC}$����$\frac{1}{2}$=$\frac{\sqrt{5}}{PC}$��
��PC=2$\sqrt{5}$��
��2���١�PEF�Ĵ�С���䣬
���ɣ���ͼ������F��FG��AD�ڵ�G��
���ı���ABFG�Ǿ��Σ�
��GF=AB=2��
�ߡ�AEP+��APE=90�㣬��GPF+��APE=90�㣬
���AEP=��GPF���֡�A=��PGF=90�㣬
���APE�ס�GFP��
��$\frac{PF}{PE}$=$\frac{GF}{AP}$=2��
����Rt��EPF�У�tan��PEF$\frac{PF}{PE}$=2����tan��PEF��ֵ���䣬
���PEF�Ĵ�С���䣻
����AE=x����EB=2-x��
��Rt��APE��PE=$\sqrt{1+{x}^{2}}$��
���ݢ��ʽ��ۣ�PF=2$\sqrt{1+{x}^{2}}$��
��EF=$\sqrt{5+5{x}^{2}}$��
�֡�PD=$\sqrt{P{C}^{2}+C{D}^{2}}$=4��
��BC=AD=5��
��BF=$\frac{1}{2}$BC=$\frac{5}{2}$��
�ࣨ$\sqrt{5+5{x}^{2}}$��2-��2-x��2=��$\frac{5}{2}$��2��
������16x2+16x-21=0��
��ã�x1=$\frac{3}{4}$��x2=-$\frac{7}{4}$����ȥ����
��AE=$\frac{3}{4}$��
���ı���AEFP�����=����ABFP�����-��EBF�����=$\frac{1}{2}$����1+$\frac{5}{2}$����2-$\frac{1}{2}$��$\frac{5}{2}$��$\frac{3}{4}$=$\frac{31}{16}$��
���߶�EF���е���������·�߳�Ϊ$\frac{1}{2}$PC=$\sqrt{5}$��
���� ���⿼����Ǿ��ε����ʡ����������ε��ж������ʡ�������Ǻ����Ķ��壬�������������ε��ж����������ʶ��������������Ǻ����Ķ����ǽ���Ĺؼ���

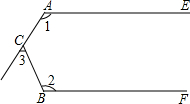 ��ͼ��ֱ��l1��l2����1=110�㣬��2=130�㣬��ô��3�Ķ����ǣ�������
��ͼ��ֱ��l1��l2����1=110�㣬��2=130�㣬��ô��3�Ķ����ǣ�������| A�� | 40�� | B�� | 50�� | C�� | 60�� | D�� | 70�� |
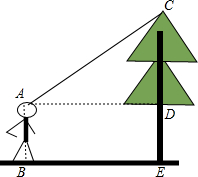 ��ͼ����һ�β�����У�С��վ�������ײ�E��5m��B����������C������Ϊ30�㣬��֪С�����۾������ľ���ABΪ1.65m����ô�������Լ�ж�ߣ��������ȷ��0.1m���ο����ݣ�$\sqrt{3}$��1.73��
��ͼ����һ�β�����У�С��վ�������ײ�E��5m��B����������C������Ϊ30�㣬��֪С�����۾������ľ���ABΪ1.65m����ô�������Լ�ж�ߣ��������ȷ��0.1m���ο����ݣ�$\sqrt{3}$��1.73�� ��ȣ�
��ȣ�
 ��ͼ����ƽ��ֱ������ϵ�У�A��-1��5����B��-1��0����C��-4��3����
��ͼ����ƽ��ֱ������ϵ�У�A��-1��5����B��-1��0����C��-4��3���� ��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ��õ������ĸ����ۣ�
��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ��õ������ĸ����ۣ�