题目内容
18.直线y=kx+b与直线y=-2x+1平行,且经过点(-2,3),则k+b=-3.分析 根据两直线平行可得出k=-2,再根据直线y=kx+b过点(-2,3)利用一次函数图象上点的坐标特征即可得出关于b的一元一次方程,解方程即可求出b值,将k、b相加即可得出结论.
解答 解:∵直线y=kx+b与直线y=-2x+1平行,
∴k=-2.
又∵直线y=kx+b过点(-2,3),
∴3=-2×(-2)+b,解得:b=-1.
∴k+b=-2-1=-3.
故答案为:-3.
点评 本题考查了两直线相交或平行问题已经一次函数图象上点的坐标特征,解题的关键是求出k和b的值.本题属于基础题,难度不大,解决该题型题目时,根据两直线平行找出一次函数一次项系数k是关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
9.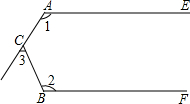 如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )
如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )
 如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )
如图,直线l1∥l2,∠1=110°,∠2=130°,那么∠3的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
10.两整式相乘的结果为a2-a-12 的是( )
| A. | (a+3)(a-4) | B. | (a-3)(a+4) | C. | (a+6)(a-2) | D. | (a-6)(a+2) |
9.化简$\sqrt{{(-2)}^{4}}$的结果为( )
| A. | 4 | B. | 16 | C. | 2 | D. | -2 |
6.某班10名学生的校服尺寸与对应人数如表所示:
则这10名学生校服尺寸的众数和中位数分别为( )
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165cm,165cm | B. | 170cm,165cm | C. | 165cm,170cm | D. | 170cm,170cm |
6.若25x2-mxy+81y2是一个完全平方式,那么m的值为( )
| A. | ±45 | B. | 90 | C. | ±90 | D. | -90 |
 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论: