题目内容
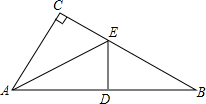 如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.(1)若∠B=28°,求∠AEC的度数;
(2)若AC=6,BC=8,求DE的长度;
(3)若AE=
| 29 |
考点:翻折变换(折叠问题)
专题:计算题
分析:(1)在Rt△ABC中,利用互余得到∠BAC=62°,再根据折叠的性质得∠CAE=
∠CAB=31°,然后根据互余可计算出∠AEC=59°;
(2)在Rt△ABC中,根据勾股定理计算出AB=10,再根据折叠的性质得AD=AC=6,CE=DE,则BD=AB-AD=4,设DE=x,则EB=BC-CE=8-x,利用勾股定理得到x2+42=(8-x)2,然后解方程;
(3)设CE=x,利用勾股定理得到AC2=AE2-CE2,AC2=AB2-BC2,则(
)2-x2=132-(x+10)2,然后解方程即可.
| 1 |
| 2 |
(2)在Rt△ABC中,根据勾股定理计算出AB=10,再根据折叠的性质得AD=AC=6,CE=DE,则BD=AB-AD=4,设DE=x,则EB=BC-CE=8-x,利用勾股定理得到x2+42=(8-x)2,然后解方程;
(3)设CE=x,利用勾股定理得到AC2=AE2-CE2,AC2=AB2-BC2,则(
| 29 |
解答:解:(1)在Rt△ABC中,∠BAC=90°-28°=62°
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴∠CAE=
∠CAB=
×62°=31°,
∴∠AEC=90°-31°=59°;
(2)在Rt△ABC中,AC=6,BC=8,
∴AB=
=10,
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴AD=AC=6,CE=DE,
∴BD=AB-AD=4,
设DE=x,则EB=BC-CE=8-x,
∵DE2+BD2=BE2,
∴x2+42=(8-x)2,解得x=3,
即DE的长为3;
(3)设CE=x,
在Rt△ACE中,CE2+AC2=AE2,即AC2=AE2-CE2,
在Rt△ACB中,BC2+AC2=AB2,即AC2=AB2-BC2,
∴(
)2-x2=132-(x+10)2,
∴x=2,
即CE的长为2.
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEC=90°-31°=59°;
(2)在Rt△ABC中,AC=6,BC=8,
∴AB=
| AC2+BC2 |
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴AD=AC=6,CE=DE,
∴BD=AB-AD=4,
设DE=x,则EB=BC-CE=8-x,
∵DE2+BD2=BE2,
∴x2+42=(8-x)2,解得x=3,
即DE的长为3;
(3)设CE=x,
在Rt△ACE中,CE2+AC2=AE2,即AC2=AE2-CE2,
在Rt△ACB中,BC2+AC2=AB2,即AC2=AB2-BC2,
∴(
| 29 |
∴x=2,
即CE的长为2.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
若0<x<1,则x,
,x2的大小关系是( )
| 1 |
| x |
A、
| ||
B、x<
| ||
C、
| ||
D、x2<x<
|
 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)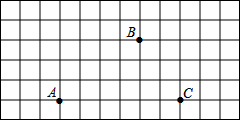 如图,A、B、C是网格图中的三点.
如图,A、B、C是网格图中的三点.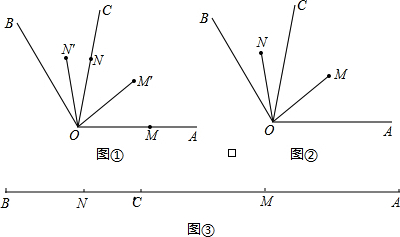
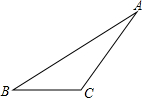 如图,在△ABC中,
如图,在△ABC中,