题目内容
10.若二次函数y=-x2+bx+c图象的对称轴是直线x=-1,且经过点(2,-1),求该二次函数的表达式.分析 由抛物线的一般形式可知:a=-1,由对称轴方程x=-$\frac{b}{2a}$,可得一个等式-$\frac{b}{2×(-1)}$=-1,可解得b=-2,然后将点(2,-1)代入y=-x2-2x+c即可得到c,可得解析式.
解答 解:∵二次函数y=-x2+bx+c图象的对称轴是直线x=-1,
∴a=-1,$-\frac{b}{2a}$=-1,
∴-$\frac{b}{2×(-1)}$=-1,
解得,b=-2,
∵二次函数y=-x2+bx+c图象经过点(2,-1),
∴-1=-22-2×2+c
解得,c=7,
∴二次函数的表达式为:y=-x2-2x+7.
点评 此题考查了用待定系数法求二次函数的解析式,解题的关键是:熟练掌握待定系数法及对称轴表达式x=-$\frac{b}{2a}$.

练习册系列答案
相关题目
18.依次连接菱形的各边中点,得到的四边形是( )
| A. | 矩形 | B. | 平行四边形 | C. | 菱形 | D. | 梯形 |
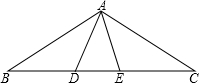 如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,求∠C的度数.
如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,求∠C的度数.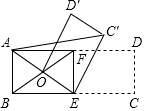 如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.
如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.