题目内容
17.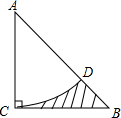 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4$\sqrt{2}$.以A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分的面积是8-2π.(结果保留π)
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4$\sqrt{2}$.以A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分的面积是8-2π.(结果保留π)
分析 根据等腰直角三角形性质求出∠A度数,解直角三角形求出AC和BC,分别求出△ACB的面积和扇形ACD的面积即可.
解答 解:∵△ACB是等腰直角三角形,∠ACB=90°,
∴∠A=∠B=45°,
∵AB=4$\sqrt{2}$,
∴AC=BC=AB×sin45°=4,
∴S△ACB=$\frac{1}{2}×AC×BC$=$\frac{1}{2}×4×4$=8,S扇形ACD=$\frac{45π•{4}^{2}}{360}$=2π,
∴图中阴影部分的面积是8-2π,
故答案为:8-2π.
点评 本题考查了扇形的面积,三角形的面积,解直角三角形,等腰直角三角形性质的应用,解此题的关键是能求出△ACB和扇形ACD的面积,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.不等式组$\left\{{\begin{array}{l}{x+1>2}\\{x-1≤2}\end{array}}\right.$的解是( )
| A. | x<1 | B. | x≥3 | C. | 1≤x<3 | D. | 1<x≤3 |
8.一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
12.一元二次方程x2-2x=0的根是( )
| A. | x1=0,x2=-2 | B. | x1=1,x2=2 | C. | x1=1,x2=-2 | D. | x1=0,x2=2 |
9.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差变大(填“变小”、“不变”或“变大”).
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 7000 |
| 木工 | 4 | 6000 |
| 瓦工 | 5 | 5000 |
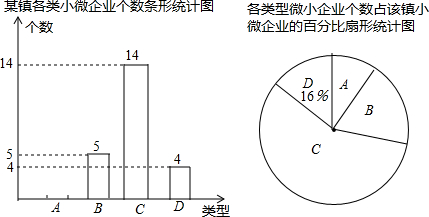
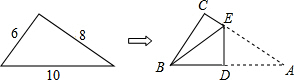 如图,一个三角形三边长为6,8,10,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长是$\frac{7}{4}$.
如图,一个三角形三边长为6,8,10,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长是$\frac{7}{4}$.