题目内容
8．一个布袋内只装有1个黑球和2个白球，这些球除颜色外其余都相同，随机摸出一个球后放回并搅匀，再随机摸出一个球，则两次摸出的球都是黑球的概率是（ ）| A． | $\frac{4}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{9}$ |
分析 列表将所有等可能的结果列举出来，利用概率公式求解即可．
解答 解：列表得：
| 黑 | 白 | 白 | |
| 黑 | （黑，黑） | （黑，白） | （黑，白） |
| 白 | （黑，白） | （白，白） | （白，白） |
| 白 | （黑，白） | （白，白） | （白，白） |
∴两次摸出的球都是黑球的概率为$\frac{1}{9}$，
故选D．
点评 本题考查了列表法与树状图法的知识，解决本题时采用了两个独立事件同时发生的概率等于两个独立事件单独发生的概率的积，难度不大．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
18．下列说法中正确的是（ ）
| A． | “打开电视，正在播放新闻节目”是必然事件 | |
| B． | “抛一枚硬币，正面向上的概率为$\frac{1}{2}$”表示每抛两次就有一次正面朝上 | |
| C． | “抛一枚均匀的正方体骰子，朝上的点数是6的概率为$\frac{1}{6}$”表示随着抛掷次数的增加，“抛出朝上的点数是6”这一事件发生的频率稳定在$\frac{1}{6}$附近 | |
| D． | 为了解某种节能灯的使用寿命，选择全面调查 |
16．
如图，正六边形ABCDEF内接于⊙O，半径为4，则这个正六边形的边心距OM和$\widehat{BC}$的长分别为（ ）
如图，正六边形ABCDEF内接于⊙O，半径为4，则这个正六边形的边心距OM和$\widehat{BC}$的长分别为（ ）| A． | 2，$\frac{π}{3}$ | B． | 2$\sqrt{3}$，π | C． | $\sqrt{3}$，$\frac{2π}{3}$ | D． | 2$\sqrt{3}$，$\frac{4π}{3}$ |
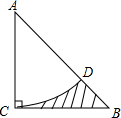如图，在等腰直角三角形ABC中，∠ACB=90°，AB=4$\sqrt{2}$．以A为圆心，AC长为半径作弧，交AB于点D，则图中阴影部分的面积是8-2π．（结果保留π）
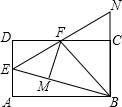如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F．将△DEF沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N，有下列四个结论：