题目内容
19.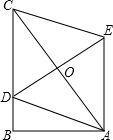 如图,在Rt△ABC中,∠B=90°,AB=3,∠BCA=30°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE最小值是3.
如图,在Rt△ABC中,∠B=90°,AB=3,∠BCA=30°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE最小值是3.
分析 由平行四边形的对角线互相平分、垂线段最短知,当OD⊥BC时,DE线段取最小值.
解答 解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD是△ABC的中位线,
∴OD=$\frac{1}{2}$AB=1.5,
∴ED=2OD=3.
故答案为:3.
点评 本题考查了平行四边形的性质,以及垂线段最短.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列各数中,不是不等式2(x-5)<x-8的解的是( )
| A. | -4 | B. | -5 | C. | -3 | D. | 5 |
14.顺次连结矩形各边的中点所得的四边形是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
11. 在A、B、C、D四幅图案中,能通过图甲平移得到的是( )
在A、B、C、D四幅图案中,能通过图甲平移得到的是( )
 在A、B、C、D四幅图案中,能通过图甲平移得到的是( )
在A、B、C、D四幅图案中,能通过图甲平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
9.使式子$\frac{\sqrt{x+1}}{x-1}$有意义的x的取值范围是( )
| A. | x>1 | B. | x≠1 | C. | x≥-1且x≠1 | D. | x>-1且x≠1 |
 尺规作图
尺规作图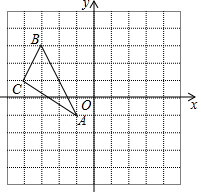 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1),画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标.
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1),画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标. 在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: