题目内容
1. 如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )| A. | $\sqrt{2015}$ | B. | $\sqrt{2016}$ | C. | $\sqrt{2017}$ | D. | $\sqrt{2018}$ |
分析 根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
解答 解:∵OP=1,OP1=$\sqrt{2}$,OP2=$\sqrt{3}$,OP3=$\sqrt{4}$=2,
∴OP4=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
…,
OP2017=$\sqrt{2018}$.
故选:D.
点评 本题考查了勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是能根据求出的结果得出规律.

练习册系列答案
相关题目
13. 如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
 如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
10.若$\sqrt{a-3}$+(b+2)2=0,则点M(a,b)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
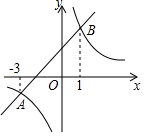 如图,双曲线y=$\frac{m}{x}$(m≠0)和直线y=x+b交于A,B两点,其横坐标分别为-3,1,则m的值是( )
如图,双曲线y=$\frac{m}{x}$(m≠0)和直线y=x+b交于A,B两点,其横坐标分别为-3,1,则m的值是( )