题目内容
7.如图1所示,一次函数y=-x-3分别交x,y轴于A,C两点,抛物线y=x2+bx+c与经过点A,C.(1)求此抛物线的函数表达式;
(2)若P为抛物线上A,C两点间的一个动点,过点P作直线x=a,交直线AC于点Q,当点P运动到什么位置时,线段PQ的长度最大?求此最大长度,及此时P点坐标;
(3)如图2在(2)条件下,直线x=-1与x轴交于N点与直线AC交于点M,当N,M,Q,D四点是平行四边形时,直接写出D点的坐标.
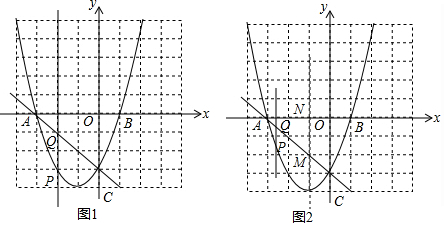
分析 (1)先求出A、C坐标,把A、C两点坐标代入y=x2+bx+c解方程组即可.
(2)设P(a,a2+2a-3),则 Q(a,-a-3),构建二次函数,利用二次函数的性质解决问题.
(3)如图2中,分两种情形①当MN为平行四边形的边时,DQ=MN=2,可得D1(-$\frac{3}{2}$,$\frac{1}{2}$),D2(-$\frac{3}{2}$,-$\frac{7}{2}$).②当MN为对角线时,可得D3(-$\frac{1}{2}$,-$\frac{1}{2}$).
解答 解:(1)∵一次函数y=-x-3分别交x,y轴于A,C两点,
∴A(-3,0)C(0,-3),把A、C两点坐标代入y=x2+bx+c
得$\left\{\begin{array}{l}{-3b+c=9}\\{b+c=-1}\end{array}\right.$ 解得$\left\{\begin{array}{l}{b=2}\\{c=-3}\end{array}\right.$,
∴y=x2+2x-3.
(2)设P(a,a2+2a-3),则 Q(a,-a-3),
∴PQ=-a-3-(a2+2a-3)=-a2-3a=-(a-$\frac{3}{2}$)2+$\frac{9}{4}$.
∴当a=-$\frac{3}{2}$时,PQ是最大值=$\frac{9}{4}$,
此时 P(-$\frac{3}{2}$,-$\frac{15}{4}$).
(3)如图2中,
∵N(-1,0),M(-1,-2),Q(-$\frac{3}{2}$,-$\frac{3}{2}$),
∴MN=2,
①当MN为平行四边形的边时,DQ=MN=2,
∴D1(-$\frac{3}{2}$,$\frac{1}{2}$),D2(-$\frac{3}{2}$,-$\frac{7}{2}$).
②当MN为对角线时,可得D3(-$\frac{1}{2}$,-$\frac{1}{2}$),
综上所述,满足条件的点D的坐标为(-$\frac{3}{2}$,$\frac{1}{2}$)或(-$\frac{3}{2}$,-$\frac{7}{2}$)或(-$\frac{1}{2}$,-$\frac{1}{2}$).
点评 本题考查二次函数、一次函数的应用、最值问题、平行四边形的判定和性质等知识,解题的关键是学会构建二次函数解决最值问题,学会分类讨论的思想思考问题,属于中考常考题型.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案| A. |  | B. |  | C. |  | D. |  |
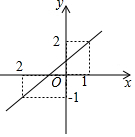 已知:一次函数的图象如图所示,
已知:一次函数的图象如图所示, 抛物线y=-x2+(m-1)x+m与y轴交点坐标是(0,3).
抛物线y=-x2+(m-1)x+m与y轴交点坐标是(0,3).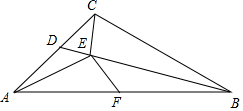 如图,等腰直角△ABC中,F为斜边AB的中点,D为AC上一点,连接BD,作CE⊥BD,垂足为E,连接AE,EF,若∠AEF=90°,求证:EF2=DE•CE.
如图,等腰直角△ABC中,F为斜边AB的中点,D为AC上一点,连接BD,作CE⊥BD,垂足为E,连接AE,EF,若∠AEF=90°,求证:EF2=DE•CE.