题目内容
2.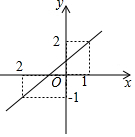 已知:一次函数的图象如图所示,
已知:一次函数的图象如图所示,(1)求直线l的解析式;
(2)求函数的图象与两坐标轴的交点坐标;
(3)判断点(3,4)是否在此函数的图象上.
分析 (1)设一次函数的解析式为y=kx+b,将点的坐标代入求出k和b的值,即可求出函数解析式;
(2)根据解析式求出函数图象与坐标轴的交点;
(3)将点的横坐标代入解析式,求得y值是否等于4,即可判断.
解答 解:(1)设函数的解析式为y=kx+b,
则$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
即解析式为:y=x+1;
(2)当x=0时,y=1,
当y=0时,x=-1,
即函数图象与坐标轴交点的坐标为:(0,1),(-1,0);
(3)将x=3代入解析式得:y=3+1=4,
故点(3,4)在此函数的图象上.
点评 此题主要考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,关键是掌握待定系数法求一次函数解析式一般步骤:
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
13.在平面直角坐标系中点A(a,4)与点B(-5,b)关于y轴对称,则2a+b的值为( )
| A. | 14 | B. | 2 | C. | -14 | D. | -2 |
10.下列四个表情图中为轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
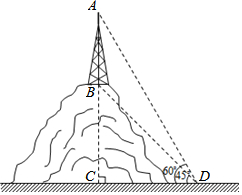 如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).
如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).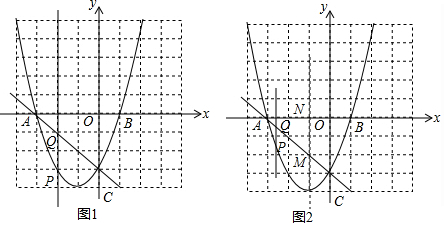
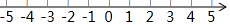
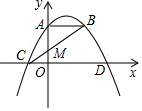 如图,点A是y轴上的点,线段AB∥x轴,M是OA的中点,连接BM并延长交x轴与点C,二次函数y=ax2-2ax+4的图象经过A,B,C的三点,与x轴的另一交点为D.
如图,点A是y轴上的点,线段AB∥x轴,M是OA的中点,连接BM并延长交x轴与点C,二次函数y=ax2-2ax+4的图象经过A,B,C的三点,与x轴的另一交点为D.