题目内容
13. 我国古代有这样一道数学题:“枯木一根直立地上,高2丈,周3尺,有葛藤自根缠绕而上,5周而达其顶.问葛藤之长几何?”这里1丈=10尺,葛藤之长指它的最短长度.解题时,枯木视为圆柱体(如图所示)周3尺指圆柱体底面周长3尺.那么葛藤的长是25尺.
我国古代有这样一道数学题:“枯木一根直立地上,高2丈,周3尺,有葛藤自根缠绕而上,5周而达其顶.问葛藤之长几何?”这里1丈=10尺,葛藤之长指它的最短长度.解题时,枯木视为圆柱体(如图所示)周3尺指圆柱体底面周长3尺.那么葛藤的长是25尺.
分析 这种立体图形求最短路径问题,可以展开成为平面内的问题解决,展开后可转化下图,所以是个直角三角形求斜边的问题,根据勾股定理可求出.
解答 解:如图,
一条直角边(即枯木的高)长20尺,
另一条直角边长5×3=15(尺),
因此葛藤长$\sqrt{2{0}^{2}+1{5}^{2}}$=25
故答案为:25.
点评 本题考查了平面展开最短路径问题,关键是把立体图形展成平面图形,本题是展成平面图形后为直角三角形按照勾股定理可求出解.

练习册系列答案
相关题目
4.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图象交于点M,则点M的坐标为( )
| A. | (-1,-2) | B. | (-1,2) | C. | (2,1) | D. | (-2,1) |
1.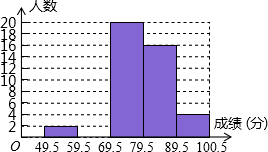 某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
(1)频数频率表中的a=8b=0.08;
(2)补全频数分布直方图;
(3)小红在班上任选一名同学,该同学数学成绩不低于80分的概率是多少?
 某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,(1)频数频率表中的a=8b=0.08;
(2)补全频数分布直方图;
(3)小红在班上任选一名同学,该同学数学成绩不低于80分的概率是多少?
| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.4 | 0.32 | b | 1 |
3.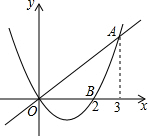 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
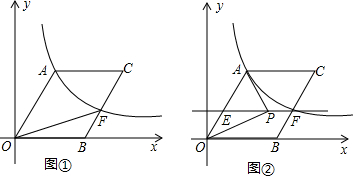
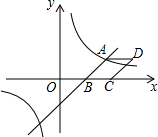 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.