题目内容
12.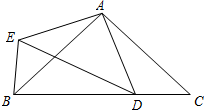 已知:如图,在△ABC中,点D在边BC上,AB=AC,∠DAE=∠BAC,AE=AD,联结DE、BE.
已知:如图,在△ABC中,点D在边BC上,AB=AC,∠DAE=∠BAC,AE=AD,联结DE、BE.(1)求证:∠ABE=∠ABC;
(2)当BE∥AD时,求证:DE=AC.
分析 (1)由∠DAE=∠BAC可知∠BAE=∠CAD,运用SSS可证明△ABE≌△ACD,即可证明结论;
(2)由(1)可知BE=CD,由BE∥AD可知∠EBD=∠ADC,∠ABE=∠BAD,由(1)知∠ABE=∠ABC,于是∠ABC=∠BAD,即可证明△ADC≌△DBE,结论可证.
解答 证明:(1)∵∠DAE=∠BAC,
∴∠BAE+∠BAD=∠BAD+∠CAD,
∴∠BAE=∠CAD,
在△ABE和△ACD中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
又∵AB=AC,
∴∠ABC=∠ACD,
∴∠ABE=∠ABC.
(2)∵△ABE≌△ACD,
∴BE=CD,
∵BE∥AD,
∴∠EBD=∠ADC,∠ABE=∠BAD,
由(1)知∠ABE=∠ABC,
∴∠ABC=∠BAD,
∴AD=DB,
在△DBE和△ACD中,
$\left\{\begin{array}{l}{AD=DB}\\{∠EBD=∠ADC}\\{BE=CD}\end{array}\right.$,
∴△DBE≌△ACD(SAS),
∴DE=AC.
点评 本题主要考查了全等三角形的判定与性质、平行线的性质、等腰三角形的性质的综合运用,根据图形分析出要证的等角和等线段所在的三角形,探索两三角形全等的条件是解决问题的关键.

练习册系列答案
相关题目
2.已知数据是1,5,6,5,5,6,6,6,则下面结论正确的是( )
| A. | 平均数是5 | B. | 中位数是5 | C. | 众数是5 | D. | 方差是5 |
20.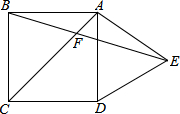 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )| A. | 75° | B. | 60° | C. | 55° | D. | 45° |
4.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图象交于点M,则点M的坐标为( )
| A. | (-1,-2) | B. | (-1,2) | C. | (2,1) | D. | (-2,1) |
1.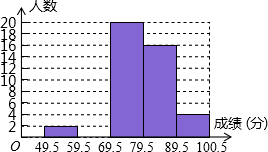 某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
(1)频数频率表中的a=8b=0.08;
(2)补全频数分布直方图;
(3)小红在班上任选一名同学,该同学数学成绩不低于80分的概率是多少?
 某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,(1)频数频率表中的a=8b=0.08;
(2)补全频数分布直方图;
(3)小红在班上任选一名同学,该同学数学成绩不低于80分的概率是多少?
| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.4 | 0.32 | b | 1 |
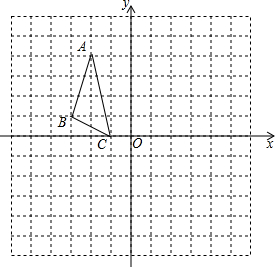 在平面直角坐标系中,△ABC的位置如图所示,其中点B(-3,1),解答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,其中点B(-3,1),解答下列问题: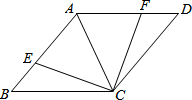 如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.
如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE=AF.求证:CE=CF.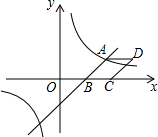 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.