题目内容
16.已知抛物线y=x2+bx+1经过点(1,0),(0,n).(1)b=-2,n=1.
(2)将该抛物线向下平移m(m>0)个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B,C,若△ABC为等边三角形.
①求m的值;
②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
分析 (1)直接把(1,0),(0,n)分别代入y=x2+bx+1可求出b和n的值;
(2)①根据抛物线的平移规律得到抛物线y=(x-1)2向下平移m(m>0)个单位所得抛物线解析式为y=(x-1)2-m,则A(1,-m),再根据抛物线与x轴的交点问题得到B(1-$\sqrt{m}$,0),C(1+$\sqrt{m}$,0),则BC=2$\sqrt{m}$,然后根据等边三角形的性质得$\frac{\sqrt{3}}{2}$•2$\sqrt{m}$=m,解得m=3;
②当m=3时,A(1,-3),抛物线解析式为y=(x-1)2-3,利用关于x轴的点的坐标特征得到D(1,3),根据平行四边形的性质得DP∥BC,DP=BC,而BC=2$\sqrt{3}$,于是可得P(1+2$\sqrt{3}$,3),然后判断P(1+2$\sqrt{3}$,3)不在抛物线y=(x-1)2-3上,于是得到不存在这样的P点.
解答 解:(1)把(1,0),(0,n)分别代入y=x2+bx+1得1+b+1=0,n=1,
所以b=-2,n=1;
故答案为-2,1;
(2)①y=x2-2x+1=(x-1)2,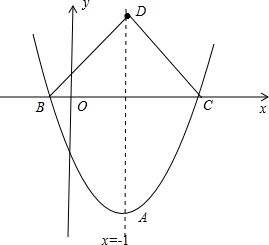
将抛物线y=(x-1)2向下平移m(m>0)个单位所得抛物线解析式为y=(x-1)2-m,则A(1,-m),
当y=0时,(x-1)2-m=0,解得x1=1+$\sqrt{m}$,x2=1-$\sqrt{m}$,则B(1-$\sqrt{m}$,0),C(1+$\sqrt{m}$,0),
∴BC=2$\sqrt{m}$,
∵△ABC为等边三角形,
∴$\frac{\sqrt{3}}{2}$•2$\sqrt{m}$=m,
∴m=3;
②不存在.理由如下:
当m=3时,A(1,-3),y=(x-1)2-3,
∵点A关于x轴的对称点为点D,
∴D(1,3),
要使四边形CBDP为平行四边形,则DP∥BC,DP=BC,
而BC=1+$\sqrt{3}$-1+$\sqrt{3}$=2$\sqrt{3}$,
∴P(1+2$\sqrt{3}$,3),
当x=1+2$\sqrt{3}$时,y=(x-1)2-3=12-3=9,
∴P(1+2$\sqrt{3}$,3)不在抛物线y=(x-1)2-3上,
∴不存在这样的P点.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等边三角形的性质和平行四边形的性质;会利用待定系数法求抛物线进行.

| A. | (-1,-2) | B. | (-1,2) | C. | (2,1) | D. | (-2,1) |
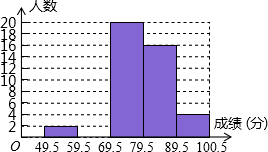 某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,
某班数学科代表小红对本班上学期期末考试成绩作了统计分析,绘制成如下频数,频率统计表和频率分布直方图.请你根据图表中提供的信息解答下列问题,(1)频数频率表中的a=8b=0.08;
(2)补全频数分布直方图;
(3)小红在班上任选一名同学,该同学数学成绩不低于80分的概率是多少?
| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.4 | 0.32 | b | 1 |
| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)(-a+b)=b2-a2 | D. | (a+b)(-a-b)=a2-b2 |
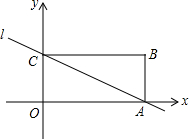 矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为y=-$\frac{2}{3}$x+2.
矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为y=-$\frac{2}{3}$x+2.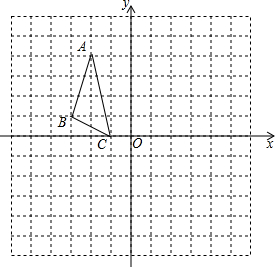 在平面直角坐标系中,△ABC的位置如图所示,其中点B(-3,1),解答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,其中点B(-3,1),解答下列问题: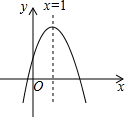 二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论: