题目内容
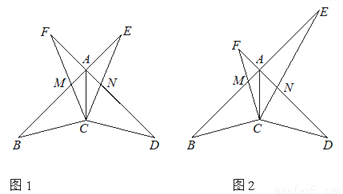
如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.
练习册系列答案
相关题目
题目内容
如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.
