��Ŀ����
 ��ͼ����ƽ��ֱ������ϵ�У�Rt��ABO��б��OA����y����������ϣ�OA��OB�ij��Ƿ���x2-6
��ͼ����ƽ��ֱ������ϵ�У�Rt��ABO��б��OA����y����������ϣ�OA��OB�ij��Ƿ���x2-6| 3 |
��1����A������꣮
��2�����ۺ�OC����ֱ�ߵĽ���ʽ��
��3����P��ֱ��OC��һ�㣬������ƽ�����Ƿ���ڵ�Q��ʹ��A��C��P��QΪ������ı�����һ�����Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���㣺һ�κ����ۺ���
ר�⣺�ۺ���
��������1�������֪���̵Ľ�õ�OA��OB�ij���ȷ����A�����꼴�ɣ�
��2����OB�ij�ΪOA����һ�룬�õ���BAO=30�㣬�����۵������ʵõ���AOC=��BOC=30�㣬��AC=OC=2x������BC=x����ֱ��������BOC�У����ù��ɶ����г�����x�ķ��̣�������̵Ľ�õ�x��ֵ��ȷ����OC�ij�����C��CE��ֱ��x�ᣬ����������Ǻ����������OE��CE�ij���ȷ����C���꣬��ֱ��OC����ʽΪy=kx����C����������k��ֵ������ȷ��������ʽ��
��3�����ڣ�������������ǣ��ٵ�P��O�غ�ʱ��C����y��ԳƵ�ΪQ������AQ��PQ����AD=PD��CD=QD����AC=PC���õ��ı���ACPQΪ���Σ������ʱQ�����ꣻ����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�䣬�ӳ�EC��Q�䣬ʹCQ��=AC������P��Q�䣬��ʱ�ı���AP��Q��CΪ���Σ����Q�����ꣻ����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�壬�ӳ�CE��Q�壬ʹCQ��=AC������P��Q�壬�ı���ACQ��P��Ϊ���Σ����Q������꣬���ϣ��õ�������������Q�����꣮
��2����OB�ij�ΪOA����һ�룬�õ���BAO=30�㣬�����۵������ʵõ���AOC=��BOC=30�㣬��AC=OC=2x������BC=x����ֱ��������BOC�У����ù��ɶ����г�����x�ķ��̣�������̵Ľ�õ�x��ֵ��ȷ����OC�ij�����C��CE��ֱ��x�ᣬ����������Ǻ����������OE��CE�ij���ȷ����C���꣬��ֱ��OC����ʽΪy=kx����C����������k��ֵ������ȷ��������ʽ��
��3�����ڣ�������������ǣ��ٵ�P��O�غ�ʱ��C����y��ԳƵ�ΪQ������AQ��PQ����AD=PD��CD=QD����AC=PC���õ��ı���ACPQΪ���Σ������ʱQ�����ꣻ����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�䣬�ӳ�EC��Q�䣬ʹCQ��=AC������P��Q�䣬��ʱ�ı���AP��Q��CΪ���Σ����Q�����ꣻ����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�壬�ӳ�CE��Q�壬ʹCQ��=AC������P��Q�壬�ı���ACQ��P��Ϊ���Σ����Q������꣬���ϣ��õ�������������Q�����꣮
��� �⣺��1������x2-6
�⣺��1������x2-6
x+24=0��
�ֽ���ʽ�ã���x-4
����x-2
��=0��
��ã�x=4
��x=2
��
��OA=4
��OB=2
��
��A��0��4
����
��2����Rt��AOB��OA=4
��OB=2
����OB=
OA��
���BAO=30�㣬��AOB=60�㣬
���۵������ʵã���AOC=��BOC=30�㣬
���BAO=��AOC=30�㣬
��AC=OC��
��Rt��BOC�У���BOC=30�㣬
��OC=2BC��
��BC=x������AC=OC=2x��
��AB=AC+CB=OC+BC=3x=
=6��
��ã�x=2��
��OC=4��
��C��CE��x����E��
��Rt��OCE�У���COE=60�㣬
���OCE=30�㣬
��OE=
OC=2��CE=
=2
��
��C��2��2
����
��ֱ��OC����ʽΪy=mx����C�������ã�2
=2m��
��ã�m=
��
��ֱ��OC����ʽΪy=
x��
��3�����ڣ������������
�����۵������ʵģ�OD=OB=2
��
��AD=OA-OD=4
-2
=2
����AD=OD��
��QΪC����y��ĶԳƵ㣬��QD=CD��
����AQ��OQ����ʱP��O�غϣ�
��AD=OD��QD=CD����AC=OC��
���ı���ACPQΪ���Σ�
��C��2��2
����
��Q��-2��2
����
����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�䣬�ӳ�EC��Q�䣬ʹCQ��=AC������P��Q�䣬
��ʱ�ı���AP��Q��CΪ���Σ�Q������Ϊ��2��2
+4����
����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�壬�ӳ�CE��Q�壬ʹCQ��=AC������P��Q�壬
�ı���ACQ��P��Ϊ���Σ���ʱQ������Ϊ��2��4-2
����
���ϣ�Q������Ϊ��-2��2
����2��2
+4����2��4-2
����
 �⣺��1������x2-6
�⣺��1������x2-6| 3 |
�ֽ���ʽ�ã���x-4
| 3 |
| 3 |
��ã�x=4
| 3 |
| 3 |
��OA=4
| 3 |
| 3 |
��A��0��4
| 3 |
��2����Rt��AOB��OA=4
| 3 |
| 3 |
| 1 |
| 2 |
���BAO=30�㣬��AOB=60�㣬
���۵������ʵã���AOC=��BOC=30�㣬
���BAO=��AOC=30�㣬
��AC=OC��
��Rt��BOC�У���BOC=30�㣬
��OC=2BC��
��BC=x������AC=OC=2x��
��AB=AC+CB=OC+BC=3x=
| OA2-OB2 |
��ã�x=2��
��OC=4��
��C��CE��x����E��
��Rt��OCE�У���COE=60�㣬
���OCE=30�㣬
��OE=
| 1 |
| 2 |
| OC2-OE2 |
| 3 |
��C��2��2
| 3 |
��ֱ��OC����ʽΪy=mx����C�������ã�2
| 3 |
��ã�m=
| 3 |
��ֱ��OC����ʽΪy=
| 3 |
��3�����ڣ������������
�����۵������ʵģ�OD=OB=2
| 3 |
��AD=OA-OD=4
| 3 |
| 3 |
| 3 |
��QΪC����y��ĶԳƵ㣬��QD=CD��
����AQ��OQ����ʱP��O�غϣ�
��AD=OD��QD=CD����AC=OC��
���ı���ACPQΪ���Σ�
��C��2��2
| 3 |
��Q��-2��2
| 3 |
����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�䣬�ӳ�EC��Q�䣬ʹCQ��=AC������P��Q�䣬
��ʱ�ı���AP��Q��CΪ���Σ�Q������Ϊ��2��2
| 3 |
����AΪԲ�ģ�AC��Ϊ�뾶��������y�ύ��P�壬�ӳ�CE��Q�壬ʹCQ��=AC������P��Q�壬
�ı���ACQ��P��Ϊ���Σ���ʱQ������Ϊ��2��4-2
| 3 |
���ϣ�Q������Ϊ��-2��2
| 3 |
| 3 |
| 3 |
��������������һ�κ����ۺ��⣬�漰��֪ʶ�У�����ϵ����ȷ��һ�κ�������ʽ��������ͼ�����ʣ����ɶ�������30��ֱ�������ε����ʣ��۵������ʣ����ε��ж������ʣ����ɶ������Լ�һԪ���η��̵Ľⷨ���������մ���ϵ�����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
x=3�Ƿ��̣��������Ľ⣮
| A��3x=6 |
| B����x-3����x-2��=0 |
| C��x��x-2��=4 |
| D��x+3=0 |
 ��ͼ����BCD�ڽ��ڡ�O��BD��ֱ����DA�ǡ�BCD��ǵ�ƽ���ߣ�AE��CD��CD���ӳ�����E��
��ͼ����BCD�ڽ��ڡ�O��BD��ֱ����DA�ǡ�BCD��ǵ�ƽ���ߣ�AE��CD��CD���ӳ�����E��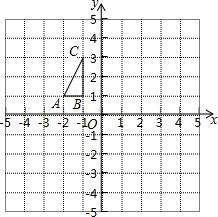 ��ͼ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ�С�����Σ�
��ͼ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ�С�����Σ� ��ͼ��AB�ǡ�O��ֱ����C��D�ڡ�O�ϣ���BC=CD����C��CE��AD����AD�ӳ�����E����AB�ӳ�����F�㣬
��ͼ��AB�ǡ�O��ֱ����C��D�ڡ�O�ϣ���BC=CD����C��CE��AD����AD�ӳ�����E����AB�ӳ�����F�㣬