题目内容
1.如图是一个正三角形场地,如果在每边上放2盆花共需要3盆花;如果在每边上放3盆花共需要6盆花,如果在每边上放4盆花,那么共需要花9盆,如果在每边上放n(n>1)盆花,那么共需要花3(n-1)盆.
分析 根据所给条件,可得当n=2时,共需要3×2-3=3×(2-1)=3盆;当n=3时,需要3×3-3=3(3-1)=6盆,当n=4时,需要3×4-3=3(4-1)=9盆,由此可以给你在每边上放n(n>1)盆花,共需要花的盆数.
解答 解:由题意可知当n=2时,共需要3×2-3=3×(2-1)=3盆;
当n=3时,需要3×3-3=3(3-1)=6盆,
当n=4时,需要3×4-3=3(4-1)=9盆,
…
所以当n=n时,需要3(n-1)盆.
故答案为9,3(n-1).
点评 本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.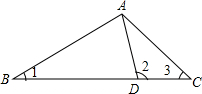 如图,在△ABC中,D是BC上一点,∠1+∠2+∠3=180°,$\frac{CD}{BD}$=$\frac{1}{3}$,则$\frac{AD}{AB}$=( )
如图,在△ABC中,D是BC上一点,∠1+∠2+∠3=180°,$\frac{CD}{BD}$=$\frac{1}{3}$,则$\frac{AD}{AB}$=( )
 如图,在△ABC中,D是BC上一点,∠1+∠2+∠3=180°,$\frac{CD}{BD}$=$\frac{1}{3}$,则$\frac{AD}{AB}$=( )
如图,在△ABC中,D是BC上一点,∠1+∠2+∠3=180°,$\frac{CD}{BD}$=$\frac{1}{3}$,则$\frac{AD}{AB}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
11.已知点A(-1,y1),B(1,y2),C(2,y3)是函数y=-$\frac{5}{x}$图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | 无法确定 |
 如图,二次函数y1=ax2+bx+c与x轴交于点A(1,0),B(3,0),且一次函数y2=mx+n过点A,与二次函数的图象相交于点C(4,4)
如图,二次函数y1=ax2+bx+c与x轴交于点A(1,0),B(3,0),且一次函数y2=mx+n过点A,与二次函数的图象相交于点C(4,4)