题目内容
12.如图(1)所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D,利用这个结论,完成下列填空.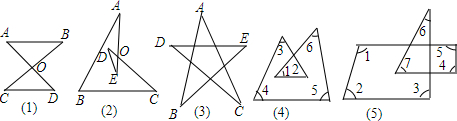
①如图(2),∠A+∠B+∠C+∠D+∠E=180°.
②如图(3),∠A+∠B+∠C+∠D+∠E=180°.
③如图(4),∠1+∠2+∠3+∠4+∠5+∠6=360°.
④如图(5),∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
分析 作出相应的辅助线,如图所示,分别利用三角形、四边形、五边形的内角和定理,利用等量代换的方法求出所求角度数即可.
解答  解:如图所示,作出相应的辅助线,
解:如图所示,作出相应的辅助线,
①如图(2),由∠D+∠E+∠DOE=∠1+∠2+∠AOC°,且∠DOE=∠AOC,
∴∠D+∠E=∠1+∠2,
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠BAO+∠B+∠OCB+∠1+∠2=180°,即∠BA0+∠B+∠OCB+∠D+∠E=180°;
②如图(3),同理得到∠D+∠E=∠DCB+∠EBC,
在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠A+∠ABE+∠EBC+∠ACD+∠DCB=180°,
即∠A+∠ABE+∠D+∠E+∠ACD=180°;
③如图(4),同理得到∠7+∠8=∠1+∠2,
由四边形内角和定理得到:∠3+∠7+∠8+∠6+∠5+∠4=360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°;
④如图(5),同理得到∠6+∠7=∠8+∠9,
由五边形内角和定理得:∠1+∠2+∠3+∠8+∠9+∠4+∠5=540°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
故答案为:①180°;②180°;③360°;④540°
点评 此题考查了三角形内角和定理,多边形内角与外角,熟练掌握内角和定理是解本题的关键.

练习册系列答案
相关题目
17.化简2$\sqrt{4+2\sqrt{3}}$-$\sqrt{21-12\sqrt{3}}$的结果为( )
| A. | 5-4$\sqrt{3}$ | B. | 4$\sqrt{3}$-1 | C. | 5 | D. | 1 |
17. 如图中,如图的几何体展开图是( )
如图中,如图的几何体展开图是( )
 如图中,如图的几何体展开图是( )
如图中,如图的几何体展开图是( )| A. |  | B. |  | C. |  | D. |  |

