题目内容
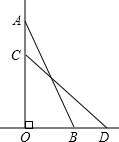
 如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,求证:∠DEC+∠DCE=90°.
如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,求证:∠DEC+∠DCE=90°.考点:平行线的性质
专题:
分析:利用平行线的性质得出∠ADB=∠CBD,进而利用三角形内角和定理得出
∠DBC+∠BDC=90°即可得出答案.
| 1 |
| 2 |
解答:
证明:∵AD∥BC,
∴∠ADB=∠CBD,
∴∠DBC+∠BDC+∠BCD=180°,
∵DE平分∠ADB,
∴∠ADE=∠EDB,
∵∠BDC=∠BCD,
∴
∠DBC+∠BDC=90°,
∴∠DEC+∠DCE=90°.
∴∠ADB=∠CBD,
∴∠DBC+∠BDC+∠BCD=180°,
∵DE平分∠ADB,
∴∠ADE=∠EDB,
∵∠BDC=∠BCD,
∴
| 1 |
| 2 |
∴∠DEC+∠DCE=90°.
点评:此题主要考查了平行线的性质以及三角形内角和定理,得出
∠DBC+∠BDC=90°是解题关键.
| 1 |
| 2 |

练习册系列答案
相关题目
将抛物线y=ax2-1(a≠0)的图象向左平移2个单位后,所得抛物线经过(1,-4)点,则a等于( )
A、-
| ||
| B、-1 | ||
| C、-3 | ||
| D、-5 |
 已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+
已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+ 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
 如图,一架25m的云梯AB斜靠在一竖直的墙AO上,这时AO为24m
如图,一架25m的云梯AB斜靠在一竖直的墙AO上,这时AO为24m 已知B,A,D在同一条直线上,∠1=∠C,∠B=40°,求∠BAE的度数.
已知B,A,D在同一条直线上,∠1=∠C,∠B=40°,求∠BAE的度数.