题目内容
 已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+
已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+| (b+c)2 |
考点:实数与数轴,二次根式的性质与化简
专题:
分析:根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的意义、二次根式的性质化简,去括号合并即可得到结果.
解答:
解:根据题意得:c<0<a<b,|b|>|c|,
可得c-b<0,a-c>0,b+c>0,
则|c-b|-|a-c|+
=b-c-a+c+b+c
=2b+c-a.
可得c-b<0,a-c>0,b+c>0,
则|c-b|-|a-c|+
| (b+c)2 |
=b-c-a+c+b+c
=2b+c-a.
点评:此题考查了整式的加减,绝对值,二次根式的性质,以及实数与数轴,涉及的知识有:去括号法则,合并同类项法则,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果函数y=(k-3)xk2-3k+2+kx+1是关于x的二次函数,那么k的值是( )
| A、1或2 | B、0或3 | C、3 | D、0 |
 如图,把边长为5cm的正方形ABCD先向右平移a cm,再向上平移b cm(a、b均小于5),得到正方形EFGH,阴影部分的面积为
如图,把边长为5cm的正方形ABCD先向右平移a cm,再向上平移b cm(a、b均小于5),得到正方形EFGH,阴影部分的面积为 如图所示,点E在AC上,∠1=∠2,∠3=∠4,试说明:BE=DE.
如图所示,点E在AC上,∠1=∠2,∠3=∠4,试说明:BE=DE.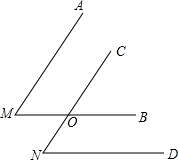 已知∠AMB和∠CND,且AM∥CN,BM∥DN,判断∠AMB与∠CND之间的数量关系.
已知∠AMB和∠CND,且AM∥CN,BM∥DN,判断∠AMB与∠CND之间的数量关系. 如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,求证:∠DEC+∠DCE=90°.
如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,求证:∠DEC+∠DCE=90°. 我国体育健儿在24届-30届奥运会上获得金牌的情况如图所示,则在这七届奥运会上,我国体育健儿共获得
我国体育健儿在24届-30届奥运会上获得金牌的情况如图所示,则在这七届奥运会上,我国体育健儿共获得