题目内容
7.当x<5时,$\frac{16}{\sqrt{5-x}}$在实数范围有意义.分析 根据二次根式的性质和分式的意义,由被开方数大于等于0,分母不等于0计算即可.
解答 解:根据二次根式的意义,被开方数5-x≥0,即x≤5;
根据分式有意义的条件,5-x≠0,解得x≠5.
所以x的取值范围是x<5,
故答案为:<5.
点评 本题考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.当二次根式在分母上时还要考虑分母不等于零,此时被开方数大于0.

练习册系列答案
相关题目
2.一个直角三角形的一条直角边长为5,斜边长为13,则另一条直角边的长是( )
| A. | 12 | B. | 10 | C. | $\sqrt{194}$ | D. | 以上答案都不是 |
16.下列运算中错误的是( )
| A. | $\frac{a}{b}$=$\frac{a{c}^{2}}{b{c}^{2}}$ | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a}{b}$=$\frac{a({k}^{2}+1)}{b({k}^{2}+1)}$ |
 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑至B.已知AB=200m,这名滑雪运动员的高度下降了100m.
如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑至B.已知AB=200m,这名滑雪运动员的高度下降了100m.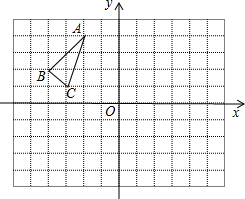 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图: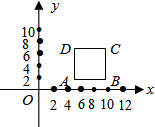 在如图所示的平面直角坐标系中有一边长为5的正方形,AB∥x轴,如果A点的坐标为(5,2),那么B点的坐标为(10,2),C点的坐标为(10,7),D点的坐标为5,7).
在如图所示的平面直角坐标系中有一边长为5的正方形,AB∥x轴,如果A点的坐标为(5,2),那么B点的坐标为(10,2),C点的坐标为(10,7),D点的坐标为5,7). 如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.
如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.