题目内容
如图,M、N为直线l上的两个动点(M在N的左侧),点A为直线l外一点,且到直线l的距离为6,∠MAN=45°.
(1)当AM=AN时,求MN的长;
(2)当AM≠AN时,作AB⊥l,垂足为B.若BM=2,求MN的长.

(1)当AM=AN时,求MN的长;
(2)当AM≠AN时,作AB⊥l,垂足为B.若BM=2,求MN的长.

考点:相似形综合题
专题:
分析:(1)如图,过点A作AB⊥MN于点B,过点M作MH⊥AN于点H.根据等腰三角形“三线合一”的性质、面积法求得AN2=6
MN.
然后在Rt△ABN中,利用勾股定理可以列出关于MN的方程,通过解方程求得MN的值;
(2)需要分类讨论:点B在点M的左侧和右侧两种情况.以点B在点M的右侧为例进行分析:通过相似三角形△MNH∽△ANB的对应边成比例得到
=
,在直角△ABM中,由勾股定理知AM=2
,则MH=
AM=2
,所以把相关线段的长度代入比例式求得BN=
AN-2.然后在Rt△ABN中,根据勾股定理得到:
36+(
AN-2)2=AN2.易求AN、BN的值.
| 2 |
然后在Rt△ABN中,利用勾股定理可以列出关于MN的方程,通过解方程求得MN的值;
(2)需要分类讨论:点B在点M的左侧和右侧两种情况.以点B在点M的右侧为例进行分析:通过相似三角形△MNH∽△ANB的对应边成比例得到
| MN |
| AN |
| MH |
| AB |
| 10 |
| ||
| 2 |
| 5 |
| ||
| 3 |
36+(
| ||
| 3 |
解答: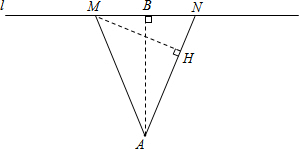 解:(1)如图,过点A作AB⊥MN于点B,过点M作MH⊥AN于点H.
解:(1)如图,过点A作AB⊥MN于点B,过点M作MH⊥AN于点H.
在Rt△MAH中,∠A=45°,
∴MH=
AM=
AN.
∵
MN•AB=
AN•MH,
∴6MN=AN•
AN,即AN2=6
MN.
在Rt△ABN中,AB2+BN2=AN2,36+(
)2=AN2
即36+(
)2=6
MN
∴MN 1=12
+12(舍去),MN 2=12
-12;
(2)如图①所示,当点B在点M右侧时.易证△MNH∽△ANB.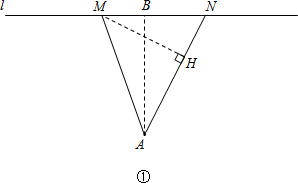
∴
=
,
∴MN•AB=AN•MH,即6MN=AN•MH.
又∵MB=2,AB=6,
∴AM=
=2
∴MH=
AM=2
,
∴6MN=2
AN,
∴6(2+BN)=2
AN.
∴BN=
AN-2.
又∵在Rt△ABN中,AB2+BN2=AN2.
即 36+(
AN-2)2=AN2.
解得:AN=3
,
∴BN=
AN-2=3.
∴MN=2+3=5.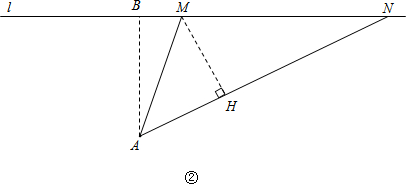
如图②所示,当点B在点M左侧时.
易证△MNH∽△ANB,
∴
=
.
∴MN•AB=AN•MH,即6MN=AN•MH.
∵MB=2,AB=6,
∴AM=
=2
,
∴MH=
AM=2
,
∴6MN=2
AN,∴6(BN-2)=2
AN,
∴BN=
AN+2.
又∵在Rt△ABN中,AB2+BN2=AN2,即36+(
AN-2)2=AN2.
解得AN=6
.
∴BN=
AN+2=12,
∴MN=12-2=10.
综上:若BM=2,MN=10或5.
 解:(1)如图,过点A作AB⊥MN于点B,过点M作MH⊥AN于点H.
解:(1)如图,过点A作AB⊥MN于点B,过点M作MH⊥AN于点H.在Rt△MAH中,∠A=45°,
∴MH=
| ||
| 2 |
| ||
| 2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴6MN=AN•
| ||
| 2 |
| 2 |
在Rt△ABN中,AB2+BN2=AN2,36+(
| MN |
| 2 |
即36+(
| MN |
| 2 |
| 2 |
∴MN 1=12
| 2 |
| 2 |
(2)如图①所示,当点B在点M右侧时.易证△MNH∽△ANB.

∴
| MN |
| AN |
| MH |
| AB |
∴MN•AB=AN•MH,即6MN=AN•MH.
又∵MB=2,AB=6,
∴AM=
| 22+62 |
| 10 |
∴MH=
| ||
| 2 |
| 5 |
∴6MN=2
| 5 |
∴6(2+BN)=2
| 5 |
∴BN=
| ||
| 3 |
又∵在Rt△ABN中,AB2+BN2=AN2.
即 36+(
| ||
| 3 |
解得:AN=3
| 5 |
∴BN=
| ||
| 3 |
∴MN=2+3=5.

如图②所示,当点B在点M左侧时.
易证△MNH∽△ANB,
∴
| MN |
| AN |
| MH |
| AB |
∴MN•AB=AN•MH,即6MN=AN•MH.
∵MB=2,AB=6,
∴AM=
| 22+62 |
| 10 |
∴MH=
| ||
| 2 |
| 5 |
∴6MN=2
| 5 |
| 5 |
∴BN=
| ||
| 3 |
又∵在Rt△ABN中,AB2+BN2=AN2,即36+(
| ||
| 3 |
解得AN=6
| 5 |
∴BN=
| ||
| 3 |
∴MN=12-2=10.
综上:若BM=2,MN=10或5.
点评:本题考查了相似综合题.此题难度较大,需要学生对相似三角形知识的综合运用能力.本题也可作∠BAC=45°,利用全等、相似,进而求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
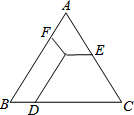 如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )| A、18 | ||
B、9
| ||
| C、6 | ||
| D、条件不够,不能确定 |
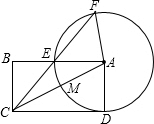 已知:如图,在矩形ABCD中,以A为圆心,AD为半径作圆并交边AC、AB于M、E,CE的延长线交⊙A于点F,且CM=2,AB=4.
已知:如图,在矩形ABCD中,以A为圆心,AD为半径作圆并交边AC、AB于M、E,CE的延长线交⊙A于点F,且CM=2,AB=4. 如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为
如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为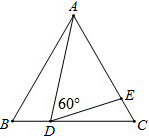 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且∠ADE=60°,若△ABC的边长为6,CD=2BD,则AD的长为
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且∠ADE=60°,若△ABC的边长为6,CD=2BD,则AD的长为