题目内容
7.已知过点A(3,4)的直线1交x,y轴于B、C两点,如果△A0B与△AOC相似,那么△BOC面积是$\frac{25}{2}$.分析 点A(3,4)的直线1交x,y轴于B、C两点,得到OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,由△A0B∽△AOC,根据相似三角形的性质得到$\frac{AO}{BO}=\frac{OC}{OA}$,于是得到OB•OC=AO2=25,代入三角形的面积公式即可得到结论.
解答 解:∵点A(3,4)的直线1交x,y轴于B、C两点,
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
当△A0B∽△AOC使,
∴$\frac{AO}{BO}=\frac{OC}{OA}$,
∴OB•OC=AO2=25,
∴S△BOC=$\frac{1}{2}$BO•OC=$\frac{1}{2}×$25=$\frac{25}{2}$,
故答案为:$\frac{25}{2}$.
点评 本题考查了相似三角形的性质,一次函数图象上的点的坐标特征,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
相关题目
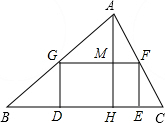 如图,在△ABC中,矩形DEFG的一边DE在BC上,另外两个顶点G,F分别在AB,AC上,高AH交GF于M,且BC=8,AH=5,矩形DEFG的周长为12.求△AGF的面积.
如图,在△ABC中,矩形DEFG的一边DE在BC上,另外两个顶点G,F分别在AB,AC上,高AH交GF于M,且BC=8,AH=5,矩形DEFG的周长为12.求△AGF的面积. 如图,已知牧马营地C和D,某一天,牧马人从营地C赶着马群,先带到草地吃草,再到河边饮水,然后回到营地D,请你替牧马人设计出最短路线.
如图,已知牧马营地C和D,某一天,牧马人从营地C赶着马群,先带到草地吃草,再到河边饮水,然后回到营地D,请你替牧马人设计出最短路线.
 的平方根是( )
的平方根是( )