题目内容
19.已知:|a-1|+(ab-2)2=0.试求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2004)(b+2004)}$的值.分析 根据非负数的性质求出a、b的值,代入所求算式计算即可.
解答 解:由题意得,a-1=0,ab-2=0,
解得a=1,b=2,
$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2004)(b+2004)}$
=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2005×2006}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2005}$-$\frac{1}{2006}$
=$\frac{2005}{2006}$.
点评 本题考查的是非负数的性质、绝对值和偶次方的非负性,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
相关题目
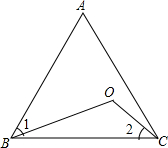 如图,O是等边三角形ABC内一点,∠1=∠2,求∠BOC的度数.
如图,O是等边三角形ABC内一点,∠1=∠2,求∠BOC的度数.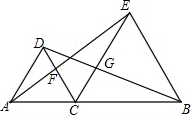 已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,AE、CD相交于F,BD、CE相交于G.求证:CF=CG.
已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,AE、CD相交于F,BD、CE相交于G.求证:CF=CG.
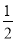 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
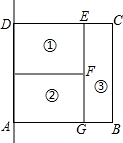 如图,某人用篱笆围成一个矩形菜园(墙壁足够长),他将矩形ABCD分为3个相等面积菜地为①、②、③,篱笆长为80m.设BC=x,ABCD面积为y,求y与x的解析式及x的取值范围,当x为多大时,y最大?
如图,某人用篱笆围成一个矩形菜园(墙壁足够长),他将矩形ABCD分为3个相等面积菜地为①、②、③,篱笆长为80m.设BC=x,ABCD面积为y,求y与x的解析式及x的取值范围,当x为多大时,y最大?