题目内容
12.小明和小芳分别转下列转盘,做配紫色游戏.(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)若出现紫色,则小明胜.此游戏的规则公平吗?试说明理由.

分析 (1)根据题意,用列表法将所有可能出现的结果,即可得答案;
(2)由(1)的表格,分析可能得到紫色的概率,得到结论.
解答 解:(1)用列表法将所有可能出现的结果表示如下:所有可能出现的结果共有12种.
| 红 | (红,红) | (蓝,红) | (黄,红) |
| 蓝 | (红,蓝) | (蓝,蓝) | (黄,蓝) |
| 红 | (红,红) | (蓝,红) | (黄,红) |
| 黄 | (红,黄) | (蓝,黄) | (黄,黄) |
| 红 | 蓝 | 黄 |
即小明获胜的概率是$\frac{1}{4}$,故小芳获胜的概率是$\frac{3}{4}$.
而$\frac{1}{4}$<$\frac{3}{4}$,
故小芳获胜的可能性大,这个“配色”游戏对双方是不公平的.
点评 本题考查的是游戏公平性的判断.实际考查概率的计算与游戏公平性的理解,要求学生根据题意,结合实际情况,计算并比较游戏者的胜利的概率,进而得到结论.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20.函数y=$\sqrt{x+2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≥-2 | C. | x≤-2 | D. | x>-2 |
7.下列四个数中,绝对值最大的是( )
| A. | 2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | -3 |
17.某地为发展教育事业,加强了对教育经费的投入,2015年投入4000万元,预计2017年投入6000万元,设教育经费的年平均增长率为x,下面所列方程正确的是( )
| A. | 4000(1+x)2=6000 | B. | 4000x2=6000 | ||
| C. | 4000(1+x%)2=6000 | D. | 4000(1+x)+4000(1+x)2=6000 |
4.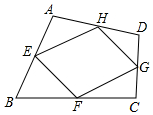 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )| A. | 20 | B. | 28 | ||
| C. | 14 | D. | 以上答案均有可能 |
1.某商品标价为a,若降价10%后出售,则实际售价为( )
| A. | 1.1a | B. | a | C. | 0.99a | D. | 0.9a |
2.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、4,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
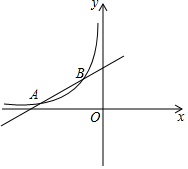 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?