题目内容
17.某地为发展教育事业,加强了对教育经费的投入,2015年投入4000万元,预计2017年投入6000万元,设教育经费的年平均增长率为x,下面所列方程正确的是( )| A. | 4000(1+x)2=6000 | B. | 4000x2=6000 | ||
| C. | 4000(1+x%)2=6000 | D. | 4000(1+x)+4000(1+x)2=6000 |
分析 设教育经费的年平均增长率为x,根据某地2015年投入教育经费4000万元,预计2017年投入6000万元可列方程.
解答 解:设教育经费的年平均增长率为x,
则2016的教育经费为:4000×(1+x)
2017的教育经费为:4000×(1+x)2.
那么可得方程:4000(1+x)2=6000.
故选A.
点评 本题考查了一元二次方程的应用,解此类题一般是根据题意分别列出不同时间按增长率所得教育经费与预计投入的教育经费相等的方程.

练习册系列答案
相关题目
7.绝对值相等的两数在数轴上对应两点的距离为8,则这两个数为( )
| A. | ±8 | B. | 0和-8 | C. | 0和8 | D. | 4和-4 |
8.4的算术平方根是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | -2 | D. | ±2 |
2.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | (-3x2y)3=-27x6y3 |
9.下列运算正确的是( )
| A. | -3-2=-1 | B. | -32=8 | C. | 2xy+xy=3xy | D. | 2x+x2=3x3 |
6.4的平方根是( )
| A. | 2 | B. | -2 | C. | 16 | D. | ±2 |
7. 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )
 古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以 看作两个相邻“三角形数”之和下列等式中符合这一规律的是( )| A. | 13=3+10 | B. | 25=9+16 | C. | 36=14+22 | D. | 49=21+28 |
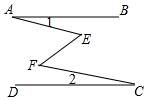 已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.
已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.