题目内容
16.观察下列数据,按某种规律在横线上填上适当的数:1,-$\frac{3}{4}$,$\frac{5}{9}$,-$\frac{7}{16}$,$\frac{9}{25}$,…,则第n个数应表示为(-1)n+1$\frac{2n-1}{n2}$.
分析 分子是从1开始连续的奇数,分母是从1开始连续自然数的平方,奇数位置为正,偶数位置为负,由此得出第n个数为(-1)n+1$\frac{2n-1}{{n}^{2}}$.
解答 解:数列为1,-$\frac{3}{4}$,$\frac{5}{9}$,-$\frac{7}{16}$,$\frac{9}{25}$,…,第n个数为(-1)n+1$\frac{2n-1}{n2}$.
故答案为(-1)n+1$\frac{2n-1}{n2}$.
点评 本题是对数字变化规律的考查,确定从分子、分母和正负情况三个方面考虑求解是解题的关键,属于中考常考题型.

练习册系列答案
相关题目
6.计算-2×3结果正确的是( )
| A. | 6 | B. | -6 | C. | 5 | D. | -5 |
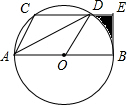 如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E.
如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E. 如图,在菱形ABCD中,AB=3,∠BAD=120°,点E从点B出发,沿BC和CD边移动,作EF⊥直线AB于点F,设点E移动的路程为x,△DEF的面积为y,则y关于x的函数图象为( )
如图,在菱形ABCD中,AB=3,∠BAD=120°,点E从点B出发,沿BC和CD边移动,作EF⊥直线AB于点F,设点E移动的路程为x,△DEF的面积为y,则y关于x的函数图象为( )



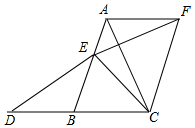 如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.
如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.