题目内容
7.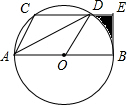 如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E.
如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E.(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长.(用含π的式子表示)
分析 (1)根据等腰三角形的性质、平行线的性质证明即可;
(2)连接BD,根据弦、弧、圆心角的关系得到∠CAD=∠CDA=∠OAD=30°,根据圆周角定理得到∠DOB=60°,根据切线的性质得到∠OBE=90°,利用弧长公式计算即可.
解答 (1)证明:∵OA=OD,
∴∠OAD=∠ODA,
∵CD∥AB,
∴∠CDA=∠OAD,
∴∠CDA=∠ODA,即DA平分∠CDO;
(2)解:连接BD,
∵AC=CD,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠CAD=∠CDA,
∵∠CDA=∠OAD,
∴∠CAD=∠CDA=∠OAD=90°×$\frac{1}{3}$=30°,
∴∠DOB=60°,
∴△BOD是等边三角形,
∴$\widehat{BD}$的长为:$\frac{60π×6}{180}$2π,
∵BE是⊙O的切线,
∴∠OBE=90°,
∴∠DBE=30°,
∵CD∥AB,∠OBE=90°,
∴∠E=90°,
∴DE=$\frac{1}{2}$BD=3,BE=BD•cos∠DBE=3$\sqrt{3}$,
∴图中阴影部分的周长为3+3$\sqrt{3}$+2π.
点评 本题考查的是切线的性质、弧长的计算,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
相关题目
17.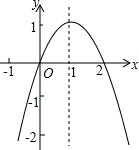 如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是( )
如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是( )
 如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是( )
如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是( )| A. | -1<a≤1 | B. | a>1 | C. | a<1 | D. | a>0 |
15.某机加工车间共有26名工人,现要加工2100个A零件,1200个B零件,已知每人每天加工A零件30个或B零件20个,问怎样分工才能确保同时完成两种零件的加工任务(每人只能加工一种零件)?设安排x人加工A零件,由题意列方程得( )
| A. | $\frac{2100}{30x}$=$\frac{1200}{20(26-x)}$ | B. | $\frac{2100}{x}$×30=$\frac{1200}{26-x}$×20 | ||
| C. | $\frac{2100}{20x}$=$\frac{1200}{30(26-x)}$ | D. | $\frac{2100}{x}$=$\frac{1200}{26-x}$ |
2.已知$\sqrt{a-2}$+(b+3)2=0,则(a+b)2017的值为( )
| A. | 0 | B. | 2017 | C. | -1 | D. | 1 |
12.在抛物线y=ax2-2ax-3a上有A(-0.5,y1)、B(2,y2)和C(3,y3)三点,若抛物线与y轴的交点在正半轴上,则y1、y2和y3的大小关系为( )
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y1<y2<y3 |
