题目内容
5.若x=$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$],求$\sqrt{{x}^{2}+1}$+x的值.分析 将x=$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$]代入原式中,利用完全平方公式可得出$\sqrt{{x}^{2}+1}$=$\frac{1}{2}$[$\sqrt{2002}$+$\frac{1}{\sqrt{2002}}$],再根据实数的加减运算即可得出结论.
解答 解:∵x=$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$],
∴原式=$\sqrt{\frac{1}{4}[\sqrt{2002}-\frac{1}{\sqrt{2002}}]^{2}+1}$+$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$],
=$\sqrt{\frac{1}{4}[\sqrt{2002}]^{2}-\frac{1}{2}+\frac{1}{4}[\frac{1}{\sqrt{2002}}]^{2}+1}$+$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$],
=$\sqrt{\frac{1}{4}[\sqrt{2002}+\frac{1}{\sqrt{2002}}]^{2}}$+$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$],
=$\frac{1}{2}$[$\sqrt{2002}$+$\frac{1}{\sqrt{2002}}$]+$\frac{1}{2}$[$\sqrt{2002}$-$\frac{1}{\sqrt{2002}}$],
=$\sqrt{2002}$.
点评 本题考查了二次根式的化简求值、完全平方公式以及实数的加减运算,利用完全平方公式将$\sqrt{{x}^{2}+1}$转化为$\frac{1}{2}$[$\sqrt{2002}$+$\frac{1}{\sqrt{2002}}$]是解题的关键.

| A. | $\frac{2100}{30x}$=$\frac{1200}{20(26-x)}$ | B. | $\frac{2100}{x}$×30=$\frac{1200}{26-x}$×20 | ||
| C. | $\frac{2100}{20x}$=$\frac{1200}{30(26-x)}$ | D. | $\frac{2100}{x}$=$\frac{1200}{26-x}$ |
| A. | 了解一批圆珠笔芯的使用寿命 | |
| B. | 了解全国中学生的节水意识 | |
| C. | 了解你们班学生早餐是否有喝奶的习惯 | |
| D. | 了解全省七年级学生的视力 |
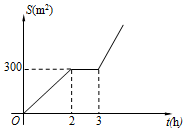 某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.
某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300. 如图所示,直角三角形AOB的周长为100,在其内部有6个小直角三角形,则这6个小直角三角形的周长之和为100.
如图所示,直角三角形AOB的周长为100,在其内部有6个小直角三角形,则这6个小直角三角形的周长之和为100.