题目内容
11. 如图,在菱形ABCD中,AB=3,∠BAD=120°,点E从点B出发,沿BC和CD边移动,作EF⊥直线AB于点F,设点E移动的路程为x,△DEF的面积为y,则y关于x的函数图象为( )
如图,在菱形ABCD中,AB=3,∠BAD=120°,点E从点B出发,沿BC和CD边移动,作EF⊥直线AB于点F,设点E移动的路程为x,△DEF的面积为y,则y关于x的函数图象为( )| A. |  | B. |  | C. |  | D. |  |
分析 分两种情形求出y与x的关系即可判断.
解答 解:①当E在BC边上时,
y=S菱形ABCD-S△BEF-S△ADF-S△DEC=2×$\frac{\sqrt{3}}{4}$×32-$\frac{1}{2}$•$\frac{x}{2}$•$\frac{\sqrt{3}}{2}$x-$\frac{1}{2}$•(3-$\frac{1}{2}$x)•$\frac{3\sqrt{3}}{2}$-$\frac{1}{2}$•(3-x)•$\frac{3\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{8}$x2+$\frac{9\sqrt{3}}{8}$x.
②当点E在CD上时,
y=$\frac{1}{2}$•(6-x)•$\frac{3\sqrt{3}}{2}$=-$\frac{3\sqrt{3}}{4}$x+$\frac{9\sqrt{3}}{2}$,
故选C.
点评 本题考查动点问题函数图象、分段函数、菱形的性质、等边三角形的性质等知识,解题的关键是学会构建分段函数解决实际问题,属于中考常考题型.

练习册系列答案
相关题目
2.已知$\sqrt{a-2}$+(b+3)2=0,则(a+b)2017的值为( )
| A. | 0 | B. | 2017 | C. | -1 | D. | 1 |
3. 如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )
如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )
 如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )
如图,方格纸中的每个小正方形的边长为1,则图中的格点四边形ABCD的面积为( )| A. | 3.5 | B. | 5 | C. | 5.5 | D. | 4.5 |
 如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(2,6),B(4,2),C(6,2).
如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(2,6),B(4,2),C(6,2).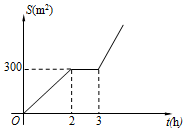 某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.
某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.