题目内容
5.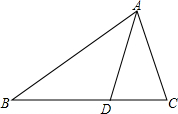 如图,AD是△ABC的角平分线,则AB:AC等于( )
如图,AD是△ABC的角平分线,则AB:AC等于( )| A. | BD:CD | B. | AD:CD | C. | BC:AD | D. | BC:AC |
分析 先过点B作BE∥AC交AD延长线于点E,由于BE∥AC,利用平行线分线段成比例定理的推论、平行线的性质,可得∴△BDE∽△CDA,∠E=∠DAC,再利用相似三角形的性质可有$\frac{BD}{CD}$=$\frac{BE}{AC}$,而利用AD时角平分线又知∠E=∠DAC=∠BAD,于是BE=AB,等量代换即可证.
解答 解:如图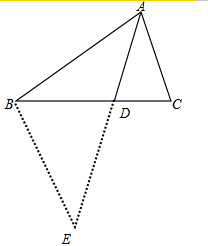
过点B作BE∥AC交AD延长线于点E,
∵BE∥AC,
∴∠DBE=∠C,∠E=∠CAD,
∴△BDE∽△CDA,
∴$\frac{BD}{CD}$=$\frac{BE}{AC}$,
又∵AD是角平分线,
∴∠E=∠DAC=∠BAD,
∴BE=AB,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$,
∴AB:AC=BD:CD.
故选:A.
点评 此题考查了角平分线的定义、相似三角形的判定和性质、平行线分线段成比例定理的推论.关键是作平行线.

练习册系列答案
相关题目
13.当a,b取任意有理数时,代数式(1)2(a+1)2+(2a-1)2;(2)a2-7a+12;(3)(4-3a)2+(b-4)2;(4)|3a-2b-4|+3a2-12a+13中,其值恒为正的有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
20.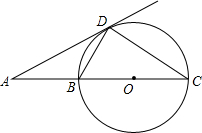 如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=$\frac{1}{2}$BC;④BD=CD,
其中正确的个数为( )
 如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB=$\frac{1}{2}$BC;④BD=CD,
其中正确的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
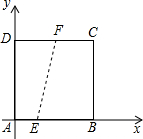 如图,已知正方形ABCD的边长为4,点E在边AB上,且AE=1;点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系.
如图,已知正方形ABCD的边长为4,点E在边AB上,且AE=1;点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系. 自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:
自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:




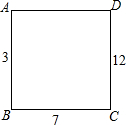 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )