题目内容
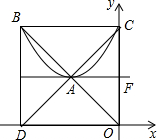 如图,点A是过点F(0,2)且和y轴垂直的直线上一点,点O是坐标原点.经过点A作OA的垂线交y轴于点C,以A为顶点且开口向上的抛物线y=a(x-h)2+2经过点C,直线OA交抛物线于另一点B,直线AC交x轴于点D,点A、B均在第二象限且互不重合.
如图,点A是过点F(0,2)且和y轴垂直的直线上一点,点O是坐标原点.经过点A作OA的垂线交y轴于点C,以A为顶点且开口向上的抛物线y=a(x-h)2+2经过点C,直线OA交抛物线于另一点B,直线AC交x轴于点D,点A、B均在第二象限且互不重合.(1)求a的值;
(2)求证:BD⊥x轴;
(3)求证:经过D、A、O三点的抛物线的顶点P在抛物线y=a(x-h)2+2上.
考点:二次函数综合题
专题:
分析:(1)根据二次函数的性质得到A(h,2),再证明Rt△OAF∽Rt△ACF,利用相似比可表示出CF=
h2,则C点坐标为(0,
h2+2),然后根据二次函数图象上点的坐标特征,把C点坐标代入抛物线解析式得到ah2+2=
h2+2,再解方程易得a=
;
(2)证明△CAF∽△CDO,利用相似比可表示出OD=-
,则D点坐标为(
,0),再利用待定系数法得到直线OA的解析式为y=
x,于是可解方程组
确定B点坐标为(
,
),然后根据点B和点D的横坐标相同即可得到BD⊥x轴;
(3)利用待定系数法可得到过点A、D、O的抛物线解析式为y=-
x2+
x,再利用抛物线顶点坐标公式得到顶点坐标为(
,
),然后根据二次函数图象上点的坐标特征可判断点(
,
)在抛物线y=a(x-h)2+2上.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明△CAF∽△CDO,利用相似比可表示出OD=-
| h2+4 |
| h |
| h2+4 |
| h |
| 2 |
| h |
|
| h2+4 |
| h |
| 2h2+8 |
| h2 |
(3)利用待定系数法可得到过点A、D、O的抛物线解析式为y=-
| 1 |
| 2 |
| h2+4 |
| 2h |
| h2+4 |
| 2h |
| h4+8h2+16 |
| 8h2 |
| h2+4 |
| 2h |
| h4+8h2+16 |
| 8h2 |
解答:(1)解:∵A点抛物线y=a(x-h)2+2的顶点,
∵A点坐标为(h,2),
∵CA⊥OA,
∴∠CAO=90°,
∴∠AOC+∠ACO=90°,
∵AF⊥y轴,
∴∠AFO=90°,
∴∠AOF+∠OAF=90°,
∴∠OAF=∠ACO,
∴Rt△OAF∽Rt△ACF,
∴
=
,即
=
,
∴CF=
h2,
∴C点坐标为(0,
h2+2),
∵抛物线y=a(x-h)2+2经过点C,
∴ah2+2=
h2+2,
∴a=
;
(2)证明:∵AF∥OD,
∴△CAF∽△CDO,
∴
=
,即
=
,
∴OD=-
,
∴D点坐标为(
,0),
设直线OA的解析式为y=kx,
把A(h,2)代入得hk=2,解得k=
,
∴直线OA的解析式为y=
x,
解方程组
得
或
,
∴B点坐标为(
,
),
∵点B和点D的横坐标相同,
∴BD⊥x轴;
(3)证明:设过点A、D、O的抛物线为y=mx(x-
),
把A(h,2)代入得mh(h-
)=2,解得m=-
,
所以过点A、D、O的抛物线解析式为y=-
x(x-
)=-
x2+
x,
顶点的横坐标为-
=
,纵坐标为
=
,
即顶点坐标为(
,
),
∵当x=
,y=
(x-h)2+2=
(
-h)2+2=
,
∴过D、A、O三点的抛物线的顶点P在抛物线y=a(x-h)2+2上.
∵A点坐标为(h,2),
∵CA⊥OA,
∴∠CAO=90°,
∴∠AOC+∠ACO=90°,
∵AF⊥y轴,
∴∠AFO=90°,
∴∠AOF+∠OAF=90°,
∴∠OAF=∠ACO,
∴Rt△OAF∽Rt△ACF,
∴
| AF |
| CF |
| OF |
| AF |
| -h |
| CF |
| 2 |
| -h |
∴CF=
| 1 |
| 2 |
∴C点坐标为(0,
| 1 |
| 2 |
∵抛物线y=a(x-h)2+2经过点C,
∴ah2+2=
| 1 |
| 2 |
∴a=
| 1 |
| 2 |
(2)证明:∵AF∥OD,
∴△CAF∽△CDO,
∴
| AF |
| OD |
| CF |
| CO |
| -h |
| OD |
| ||
|
∴OD=-
| h2+4 |
| h |
∴D点坐标为(
| h2+4 |
| h |
设直线OA的解析式为y=kx,
把A(h,2)代入得hk=2,解得k=
| 2 |
| h |
∴直线OA的解析式为y=
| 2 |
| h |
解方程组
|
|
|
∴B点坐标为(
| h2+4 |
| h |
| 2h2+8 |
| h2 |
∵点B和点D的横坐标相同,
∴BD⊥x轴;
(3)证明:设过点A、D、O的抛物线为y=mx(x-
| h2+4 |
| h |
把A(h,2)代入得mh(h-
| h2+4 |
| h |
| 1 |
| 2 |
所以过点A、D、O的抛物线解析式为y=-
| 1 |
| 2 |
| h2+4 |
| h |
| 1 |
| 2 |
| h2+4 |
| 2h |
顶点的横坐标为-
| ||
2×(-
|
| h2+4 |
| 2h |
0-(
| ||
4×(-
|
| h4+8h2+16 |
| 8h2 |
即顶点坐标为(
| h2+4 |
| 2h |
| h4+8h2+16 |
| 8h2 |
∵当x=
| h2+4 |
| 2h |
| 1 |
| 2 |
| 1 |
| 2 |
| h2+4 |
| 2h |
| h4+8h2+16 |
| 8h2 |
∴过D、A、O三点的抛物线的顶点P在抛物线y=a(x-h)2+2上.
点评:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质以及二次函数图象与一次函数图象的交点坐标的求法;熟练运用相似比计算线段的长和代数式的变形;理解坐标与图形性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
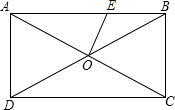 如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD=
如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD= 抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.
抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.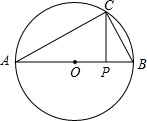 如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合),试判断PA、PB、PC的大小关系,并说明理由.
如图所示,在⊙O上有一点C(C不与A、B重合),在直径AB上有一个动点P(P不与A、B重合),试判断PA、PB、PC的大小关系,并说明理由.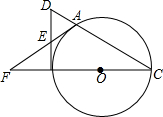 如图,A是以BC为直径的⊙O上一点,过点B作圆O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.
如图,A是以BC为直径的⊙O上一点,过点B作圆O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.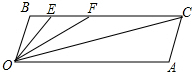 如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.
如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.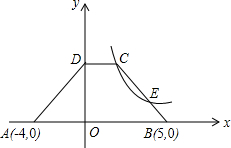 如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=
如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=