题目内容
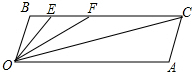 如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.
如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.(1)∠EOC=
(2)若平行移动AC,那么∠OCB与∠OFB大小的比值是否会发生变化?若变化,试说明理由;若不变,请求出这个比值;
(3)在平行移动AC的过程中,若点P是射线OE上一点(点P不与O、E两点重合),过点P作PQ⊥BC于点Q,设∠OFB=α,请用含α的代数式表示∠EPQ,并说明理由.
考点:平行线的性质,三角形内角和定理,三角形的外角性质
专题:
分析:(1)由BC∥OA得∠B+∠O=180°,所以∠O=180°-∠B=80°,则∠A+∠O=180°,根据平行线的判定即可得到OB∥AC;
(2)由OE平分∠BOF得到∠BOE=∠FOE,加上∠FOC=∠AOC,所以∠EOF+∠COF=
∠AOB=40°;
(3)分类讨论:当点P在线段OE上时,当点P在线段OE的延长线上时,
①根据三角形内角和,可得∠BOF=80°-α,根据角平分线的性质,可得∠EOF=40°-
α,根据三角形的外角的性质,可得∠OEB=40°+
α,根据直角三角形的性质,可得答案;
②根据三角形内角和,可得∠BOF=80°-α,根据角平分线的性质,可得∠EOF=40°-
α,根据对顶角的性质,可得∠PEQ=∠OEB=40°+
α,根据直角三角形的性质,可得答案.
(2)由OE平分∠BOF得到∠BOE=∠FOE,加上∠FOC=∠AOC,所以∠EOF+∠COF=
| 1 |
| 2 |
(3)分类讨论:当点P在线段OE上时,当点P在线段OE的延长线上时,
①根据三角形内角和,可得∠BOF=80°-α,根据角平分线的性质,可得∠EOF=40°-
| 1 |
| 2 |
| 1 |
| 2 |
②根据三角形内角和,可得∠BOF=80°-α,根据角平分线的性质,可得∠EOF=40°-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)40°;
(2)不变,理由如下:
∵CB∥OA,
∴∠OCB=∠COA,∠OFB=∠FOA,
∵∠FOC=∠AOC,
∴∠COA=
∠FOA,即∠OCB:∠OFB=1:2.
(3)∠EPQ=50°-
α,
理由:当点P在线段OE上时,如图1:
 ,
,
∵∠B+∠BOF+∠BFO=180°,且∠B=100°,∠OFB=α,
∴∠BOF=180°-100°-α=80°-α
∵OE平分∠BOF,∴∠EOF=
∠BOF
即∠EOF=
(80°-α)=40°-
α
∵∠OEB=∠EOF+∠OFB=40°-
α+α=40°+
α
∴∠EPQ=90°-∠OEB=90°-(40°+
∠α)=50°-
α
即∠EPQ=50°-
α
当点P在线段OE的延长线上时,如图2:
 ,
,
由上述说理过程知:∠OEB=40°+
α
∵∠PEQ=∠OEB=40°+
α
∴∠EPQ=90°-∠PEQ=90°-(40°+
∠α)=50°-
α
即∠EPQ=50°-
α
综上所述:∠EPQ=50°-
α.
(2)不变,理由如下:
∵CB∥OA,
∴∠OCB=∠COA,∠OFB=∠FOA,
∵∠FOC=∠AOC,
∴∠COA=
| 1 |
| 2 |
(3)∠EPQ=50°-
| 1 |
| 2 |
理由:当点P在线段OE上时,如图1:
 ,
,∵∠B+∠BOF+∠BFO=180°,且∠B=100°,∠OFB=α,
∴∠BOF=180°-100°-α=80°-α
∵OE平分∠BOF,∴∠EOF=
| 1 |
| 2 |
即∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OEB=∠EOF+∠OFB=40°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EPQ=90°-∠OEB=90°-(40°+
| 1 |
| 2 |
| 1 |
| 2 |
即∠EPQ=50°-
| 1 |
| 2 |
当点P在线段OE的延长线上时,如图2:
 ,
,由上述说理过程知:∠OEB=40°+
| 1 |
| 2 |
∵∠PEQ=∠OEB=40°+
| 1 |
| 2 |
∴∠EPQ=90°-∠PEQ=90°-(40°+
| 1 |
| 2 |
| 1 |
| 2 |
即∠EPQ=50°-
| 1 |
| 2 |
综上所述:∠EPQ=50°-
| 1 |
| 2 |
点评:本题考查了平行线的性质,利用了平行线的性质,三角形的内角和定理,角平分线的性质,直角三角形的性质,综合性较强.

练习册系列答案
相关题目
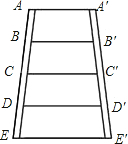 如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60cm,EE′=80cm.则BB′的长为( )
如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60cm,EE′=80cm.则BB′的长为( )| A、0.65m |
| B、0.675m |
| C、0.725m |
| D、0.75m |
数据1,2,3,4,3的众数是( )
| A、1 | B、2 | C、3 | D、4 |
用一个经过正方体上、下两面对角线的平面截该正方体,截面是( )
| A、三角形 | B、正方形 |
| C、长方形 | D、梯形 |
 如图,点A是过点F(0,2)且和y轴垂直的直线上一点,点O是坐标原点.经过点A作OA的垂线交y轴于点C,以A为顶点且开口向上的抛物线y=a(x-h)2+2经过点C,直线OA交抛物线于另一点B,直线AC交x轴于点D,点A、B均在第二象限且互不重合.
如图,点A是过点F(0,2)且和y轴垂直的直线上一点,点O是坐标原点.经过点A作OA的垂线交y轴于点C,以A为顶点且开口向上的抛物线y=a(x-h)2+2经过点C,直线OA交抛物线于另一点B,直线AC交x轴于点D,点A、B均在第二象限且互不重合. 如图,BC⊥AE,垂足为C,过点C作CD∥AB,若∠ECD=51°,则∠B的度数为
如图,BC⊥AE,垂足为C,过点C作CD∥AB,若∠ECD=51°,则∠B的度数为 如图,双曲线y1=
如图,双曲线y1=