题目内容
9.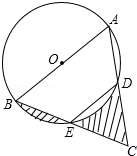 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 首先证明△ABC是等边三角形.则△EDC是等边三角形,边长是2.而$\widehat{BE}$和弦BE围成的部分的面积=$\widehat{DE}$和弦DE围成的部分的面积,据此即可求解.
解答 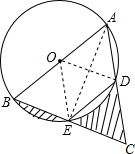 解:连接AE,OD、OE.
解:连接AE,OD、OE.
∵AB是直径,
∴∠AEB=90°,
又∵∠BED=120°,
∴∠AED=30°,
∴∠AOD=2∠AED=60°.
∵OA=OD,
∴△AOD是等边三角形,
∴∠OAD=60°,
∵点E为BC的中点,∠AEB=90°,
∴AB=AC,
∴△ABC是等边三角形,边长是8,△EDC是等边三角形,边长是4,
∴∠BOE=∠EOD=60°,
∴$\widehat{BE}$和弦BE围成的部分的面积=$\widehat{DE}$和弦DE围成的部分的面积,
∴阴影部分的面积=S△EDC=$\frac{\sqrt{3}}{4}$×42=4$\sqrt{3}$.
故选A.
点评 本题考查了等边三角形的面积的计算,证明△EDC是等边三角形,边长是4.理解$\widehat{BE}$和弦BE围成的部分的面积=$\widehat{DE}$和弦DE围成的部分的面积是关键.

练习册系列答案
相关题目
19.下列各数中,无理数是( )
| A. | $\sqrt{4}$ | B. | 3.14 | C. | $\root{3}{-27}$ | D. | 5π |
17.在正五边形、正六边形、正七边形、正八边形中,若只用同一种正多边形铺满地面,则可供选择的正多边形为( )
| A. | 正五边形 | B. | 正六边形 | C. | 正七边形 | D. | 正八边形 |
14.下列说法中,正确的是( )
| A. | 任意两个矩形形状相似 | B. | 任意两个菱形形状相似 | ||
| C. | 任意两个直角三角形形状相似 | D. | 任意两个正五边形形状相似 |
16.在一次社会调查活动中,小明调查了一个路口的车流量,具体数据如下:
在这组数据中,众数和中位数依次是( )
| 时间段 | 7~8点 | 8~9点 | 9~10点 | 10~11点 | 11~12点 |
| 数量/辆 | 68 | 56 | 50 | 68 | 54 |
| A. | 56,68 | B. | 68,56 | C. | 68,55 | D. | 68,50 |
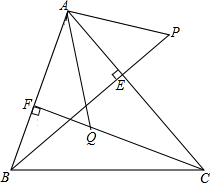 如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.