题目内容
16.在一次社会调查活动中,小明调查了一个路口的车流量,具体数据如下:| 时间段 | 7~8点 | 8~9点 | 9~10点 | 10~11点 | 11~12点 |
| 数量/辆 | 68 | 56 | 50 | 68 | 54 |
| A. | 56,68 | B. | 68,56 | C. | 68,55 | D. | 68,50 |
分析 众数是一组数据中出现次数最多的数据,注意众数可以不止一个;中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
解答 解:68出现的次数最多,众数为68.
这组数据按大小顺序排列为50,54,56,68,68第3数是56,所以中位数为56.
故选B.
点评 本题属于基础题,考查了确定一组数据的中位数和众数的能力,要明确定义,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.

练习册系列答案
相关题目
9.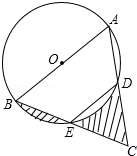 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
11.在△ABC中,∠ACB=90°,AC=1,BC=2,则下列说法正确的是( )
| A. | ∠B=30° | B. | 斜边上的中线长为1 | ||
| C. | 该三角形外接圆的半径为1 | D. | 斜边上高线长为$\frac{2}{5}\sqrt{5}$ |
8.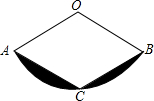 如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
 如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-2$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\sqrt{3}$ | D. | $\frac{4π}{3}$-2$\sqrt{3}$ |
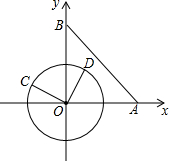 在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB
在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB