题目内容
4.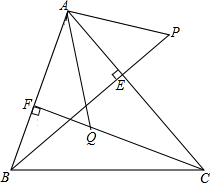 如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
如图,已知BE,CF是△ABC的高,P为BE延长线上的-点,Q为CF上一点,△PAB≌△AQC,且AB与QC是对应边,试说明AP⊥AQ.
分析 由全等三角形的性质得出对应边相等AP=AQ,对应角相等∠P=∠QAC,再由BE⊥AC,根据互余两角的关系得出∠QAC+∠PAE=90°,即可得出结论.
解答 证明:∵△PAB≌△AQC,
∴AP=AQ,∠P=∠QAC,
∵BE⊥AC,
∴∠AEP=90°,
∴∠P+∠PAE=90°,
∴∠QAC+∠PAE=90°,
即∠PAQ=90°,
∴AP⊥AQ.
点评 本题考查了全等三角形的性质、互余两角的关系、垂线的判定;熟练掌握全等三角形的性质是解决问题的关键.

练习册系列答案
相关题目
19.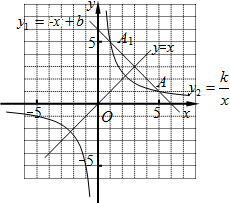 如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.由图象可得不等式$\frac{k}{x}$+x-b≥0的解是( )
如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.由图象可得不等式$\frac{k}{x}$+x-b≥0的解是( )
 如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.由图象可得不等式$\frac{k}{x}$+x-b≥0的解是( )
如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.由图象可得不等式$\frac{k}{x}$+x-b≥0的解是( )| A. | x≥5 | B. | 0<x≤-1 | C. | 1≤x≤5 | D. | x≥5或 0<x≤1 |
9.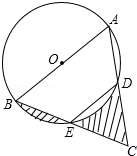 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
11.在△ABC中,∠ACB=90°,AC=1,BC=2,则下列说法正确的是( )
| A. | ∠B=30° | B. | 斜边上的中线长为1 | ||
| C. | 该三角形外接圆的半径为1 | D. | 斜边上高线长为$\frac{2}{5}\sqrt{5}$ |
 如图,AB∥CD,如果∠1=110°,∠3=30°,那么∠2=100°.
如图,AB∥CD,如果∠1=110°,∠3=30°,那么∠2=100°.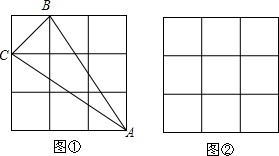
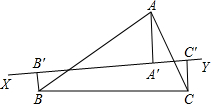 如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′.
如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′.