题目内容
1.已知a、b、c是△ABC的三边,且a=4,b=6.若三角形的周长是小于16的偶数.(1)求第三边c的长;
(2)求△ABC的周长.
分析 (1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)利用三角形周长的定义得出即可.
解答 解:(1)∵a,b,c是△ABC的三边,a=4,b=6,
∴2<c<10,
∵三角形的周长是小于16的偶数,
∴2<c<6,
∴c=4;
(2)当c=4时,△ABC的周长为4+6+4=14.
点评 此题主要考查了三角形周长的定义和三角形三边关系,得出c的取值范围是解题关键.

练习册系列答案
相关题目
9.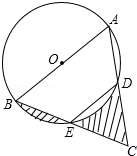 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
8.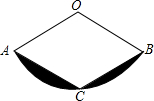 如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
 如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-2$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\sqrt{3}$ | D. | $\frac{4π}{3}$-2$\sqrt{3}$ |

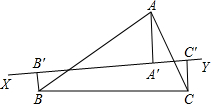 如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′.
如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′. 如图中,正方形ABCD和EFGH,下图中有哪些全等形并证明.
如图中,正方形ABCD和EFGH,下图中有哪些全等形并证明.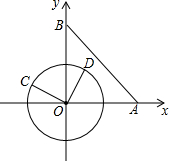 在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB
在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB