题目内容
18.有理数a、b、c不为0,且a+b+c=0,设x=|$\frac{|a|}{b+c}$+$\frac{|b|}{c+a}$+$\frac{|c|}{a+b}$|,求x19+2x+13的值.分析 根据题意可得a,b,c中不能全同号,必有一正两负或两正一负与a=-(b+c),b=-(c+a),c=-(a+b),则可得|$\frac{|a|}{b+c}$,$\frac{|b|}{c+a}$,$\frac{|c|}{a+b}$|的值为两个+1,一个-1或两个-1,一个+1,即可求得x的值,代入即可求得答案.
解答 解:∵有理数a,b,c均不为0,且a+b+c=0,
∴a,b,c中不能全同号,必有一正两负或两正一负,
∴a=-(b+c),b=-(c+a),c=-(a+b),
即$\frac{a}{b+c}$=-1,$\frac{b}{c+a}$=-1,$\frac{c}{a+b}$=-1
∴|$\frac{|a|}{b+c}$,$\frac{|b|}{c+a}$,$\frac{|c|}{a+b}$|的值中必有两个同号,另一个符号与其相反,
∴|$\frac{|a|}{b+c}$,$\frac{|b|}{c+a}$,$\frac{|c|}{a+b}$|的值为两个+1,一个-1或两个-1,一个+1,
∴x=1,
∴原式=1+2+13=16.
点评 本题考查了分式的运算,注意分类讨论思想的应用,能得到|$\frac{|a|}{b+c}$,$\frac{|b|}{c+a}$,$\frac{|c|}{a+b}$|的值为两个+1,一个-1或两个-1,一个+1是解此题的关键.

练习册系列答案
相关题目
8.下列结论正确的是( )
| A. | 所有正五边形都相似 | B. | 所有平行四边形都相似 | ||
| C. | 所有菱形都相似 | D. | 所有长方形都相似 |
9.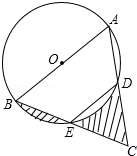 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
 如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=8,∠BED=120°,则图中阴影部分的面积之和为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
 如图中,正方形ABCD和EFGH,下图中有哪些全等形并证明.
如图中,正方形ABCD和EFGH,下图中有哪些全等形并证明.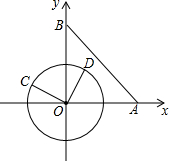 在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB
在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB