题目内容
17.小明在解决问题:已知a=$\frac{1}{2+\sqrt{3}}$,求2a2-8a+1的值.他是这样分析与解的:∵a=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$,
∴a-2=-$\sqrt{3}$,
∴(a-2)2=3,a2-4a+4=3
∴a2-4a=1,
∴a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)化简$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{121}+\sqrt{119}}$
(2)若a=$\frac{1}{\sqrt{2}-1}$,①求4a2-8a+1的值;
②直接写出代数式的值a3-3a2+a+1=0; 2a2-5a+$\frac{1}{a}$+2=2.
分析 (1)将原式分母有理化即可;
(2)将a分母有理化,化简为$\sqrt{2}+1$,代入①,②进行运算即可.
解答 解:(1)原式=$\frac{1}{2}$×($\sqrt{3}-1$+$\sqrt{5}$$-\sqrt{3}$+$\sqrt{7}$$-\sqrt{5}$+…+$\sqrt{121}$$-\sqrt{119}$)
=$\frac{1}{2}$×($\sqrt{121}$-1)
=$\frac{1}{2}×$10
=5;
(2)①∵a=$\sqrt{2}+1$,
∴4a2-8a+1
=4×${(\sqrt{2}+1)}^{2}$-8×($\sqrt{2}+$1)+1
=5;
②a3-3a2+a+1
=${(\sqrt{2}+1)}^{3}$-3${(\sqrt{2}+1)}^{2}$+($\sqrt{2}+1$)+1
=7+5$\sqrt{2}$-(9$+6\sqrt{2}$)+$\sqrt{2}$+1+1
=0;
2a2-5a+$\frac{1}{a}$+2
=2×${(\sqrt{2}+1)}^{2}$$-5(\sqrt{2}+1)$+$\sqrt{2}-1$+2
=2;
故答案为:0,2.
点评 本题主要考查了分母有理化,利用分母有理化化简是解答此题的关键.

练习册系列答案
相关题目
12. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
 如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠BCD=35°,则∠ABD的度数为( )| A. | 65° | B. | 35° | C. | 55° | D. | 60° |
9.三角形的内心是( )
| A. | 三边垂直平分线的交点 | B. | 三条角平分线的交点 | ||
| C. | 三条高所在直线的交点 | D. | 三条中线的交点 |
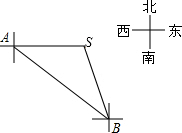 为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)
为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)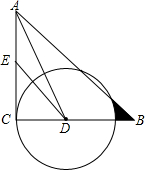 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线BC于点D,E是AC上一点,DE=DB,以D为圆心,DC为半径作⊙D
如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线BC于点D,E是AC上一点,DE=DB,以D为圆心,DC为半径作⊙D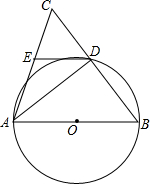 如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.
如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.