如果两个角的两边分别平行.其中一个角比另一个角的2倍少36°.那么这两个角是36°.36°或72°.108°．题目和参考答案——青夏教育精英家教网—

题目内容

2．如果两个角的两边分别平行，其中一个角比另一个角的2倍少36°，那么这两个角是36°，36°或72°，108°．

分析由两个角的两边分别平行，可得这两个角相等或互补，可设其中一个角为x°，由其中一个角比另一个角的2倍少36°，分别从这两个角相等或互补去分析，即可列方程，解方程即可求得这两个角的度数．

解答解：∵两个角的两边分别平行，
∴这两个角相等或互补，
设其中一个角为x°，
∵其中一个角比另一个角的2倍少36°，
①若这两个角相等，则2x-x=36，
解得：x=36，
∴这两个角的度数分别为36°，36°；
②若这两个角互补，则2（180-x）-x=36，
解得：x=108，
∴这两个角的度数分别为108°，72°；
综上，这两个角的度数分别为36°，36°或72°，108°．
故答案为：36°，36°或72°，108°．

点评此题考查了平行线的性质．此题难度适中，解题的关键是注意由两个角的两边分别平行，可得这两个角相等或互补，注意分类讨论思想的应用．

练习册系列答案

13．已知点A（n²+1，n）在正比例函数y=-2x的图象上，则（　　）

10．设a，b，c△ABC的三边长，则$\sqrt{（a+b-c）^{2}}$+|a-b-c|=（　　）

17．小明在解决问题：已知a=$\frac{1}{2+\sqrt{3}}$，求2a²-8a+1的值．他是这样分析与解的：∵a=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{（2+\sqrt{3}）（2-\sqrt{3}）}$=
2-$\sqrt{3}$，
∴a-2=-$\sqrt{3}$，
∴（a-2）²=3，a²-4a+4=3
∴a²-4a=1，
∴a²-8a+1=2（a²-4a）+1=2×（-1）+1=-1．
请你根据小明的分析过程，解决如下问题：
（1）化简$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{121}+\sqrt{119}}$
（2）若a=$\frac{1}{\sqrt{2}-1}$，①求4a²-8a+1的值；
②直接写出代数式的值a³-3a²+a+1=0； 2a²-5a+$\frac{1}{a}$+2=2．

7．工人师傅准备从一块面积为25平方分米的正方形工料上裁剪出一块18平方分米的长方形的工件．
（1）求正方形工料的边长；
（2）若要求裁下来的长方形的长宽的比为3：2，问这块正方形工料是否合格？
（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，$\sqrt{5}$≈2.236）

14．

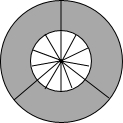如图是由三把相同大小的扇子展开后组成的图形，若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”（　　）

	A．	平移一次形成的
	B．	平移两次形成的
	C．	以轴心为旋转中心，旋转120°后形成的
	D．	以轴心为旋转中心，旋转120°、240°后形成的

11．（1）如图1，平面内有一等腰直角三角板ABC（∠ACB=90°）和一直线MN．过点C作CE⊥MN于点E，过点B作BF⊥MN于点F，试证明线段AF，BF，CE之间的数量关系为AF+BF=2CE．（提示：过点C作BF的垂线，利用三角形全等证明．）
（2）若三角板绕点A顺时针旋转至图2的位置，其他条件不变，试猜想线段AF、BF、CE之间的数量关系，并证明你的猜想．
（3）若三角板绕点A顺时针旋转至图3的位置，其他条件不变，则线段AF、BF、CE之间的数量关系为BF-AF=2CE

12．一个平行四边形被两条对角线分为四个小三角形，其中两个形状不同的三角形的周长和为80cm，两条对角线的长度之比为2：3，若这个平行四边形的周长为68cm，则两条对角线的长度分别为18.4cm，27.6cm．

试题分类