题目内容
7.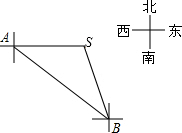 为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)
为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 过点S作SC⊥AB,C为垂足.先解Rt△ACS,由∠CAS=45°,AS=80$\sqrt{2}$,得出SC=AC=80.再解Rt△BCS,由∠CBS=45°-15°=30°,得出BC=80$\sqrt{3}$,那么AB=AC+BC=80+80$\sqrt{3}$,然后根据速度=路程÷时间即可求出该舰艇的巡航速度.
解答  解:过点S作SC⊥AB,C为垂足.
解:过点S作SC⊥AB,C为垂足.
∵在Rt△ACS中,∠CAS=45°,AS=80$\sqrt{2}$,
∴SC=AC=80.
∵在Rt△BCS中,∠CBS=45°-15°=30°,
∴BC=80$\sqrt{3}$,
∴AB=AC+BC=80+80$\sqrt{3}$,
∴该舰艇的巡航速度是(80+80$\sqrt{3}$)÷(11-9)=40+40$\sqrt{3}$≈109(海里/时).
答:该舰艇的巡航速度约为109海里/时.
点评 本题考查了解直角三角形的应用-方向角问题,准确作出辅助线构造直角三角形是解决本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
15.下面是某次数学测验同学们的计算摘录,其中正确的是( )
| A. | 2a+3b=5ab | B. | (-2a2)3=6a6 | C. | a3•a2=a6 | D. | -a5÷(-a)=a4 |
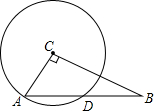 如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
 如图,菱形ABCD的对角线AC、BD交于点O,E为边BC的中点,若OE=6cm,则菱形ABCD的周长为48cm.
如图,菱形ABCD的对角线AC、BD交于点O,E为边BC的中点,若OE=6cm,则菱形ABCD的周长为48cm.