题目内容
6．
如图，一次函数y=kx+6的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=$\frac{n}{x}$（x＜0）的图象在第二象限交于点C，CD⊥x轴，垂足为D，且OB：OA：OD=6：3：2（1）求一次函数与反比例函数的解析式；
（2）当kx+6≤$\frac{n}{x}$时，请直接写出x的取值范围．
分析 （1）求出OB=6，求出A、B的坐标，把A的坐标代入y=kx+6求出k，即可得出一次函数的解析式，求出C的坐标，即可得出反比例函数的解析式；
（2）根据C的坐标和图象得出答案即可．
解答 解：（1）y=kx+6，
当x=0时，y=6，
即OB=6，
∵OB：OA：OD=6：3：2，
∴OA=3，OD=2，
即A的坐标为（3，0），
把A的坐标代入y=kx+6得：k=-2，
即一次函数的解析式为y=-2x+6，
把x=-2代入y=-2x+6得：y=10，
即C的坐标为（-2，10），
把C的坐标代入y=$\frac{n}{x}$得：n=-20，
∴反比例函数的解析式为y=-$\frac{20}{x}$；
（2）当kx+6≤$\frac{n}{x}$时，x的取值范围是-2≤x＜0．
点评 本题考查了一次函数和反比例函数的交点问题，用待定系数法求函数的解析式等知识点，能正确用待定系数法求出函数的解析式是解此题的关键，注意数形结合思想的运用．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（-4，8），对角线AC⊥x轴于点C，点D在y轴上，求直线AB的解析式．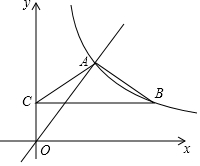
如图，函数y=$\frac{4}{3}$x与函数y=$\frac{m}{x}$（x＞0）的图象相交于点A（n，4）．点B在函数y=$\frac{m}{x}$（x＞0）的图象上，过点B作BC∥x轴，BC与y轴相交于点C，且AB=AC．
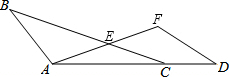如图，点A，C，D在同一条直线上，BC与AF交于点E，AF=AC，AD=BC，AE=EC．
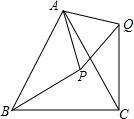如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ．判断△APQ的形状，并说明理由．
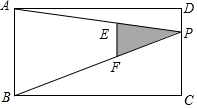一只小狗在如图所示的矩形草地ABCD内自由的玩耍，点P是矩形的边CD上一点，点E、点F分别为PA，PB的中点，连接EF，则这只小狗跑到△PEF内的概率是$\frac{1}{8}$．
如图，在?ABCD中，点E在边BC上，点F在边AD上，且BE=DF，连结AE、CF．求证：四边形AECF是平行四边形．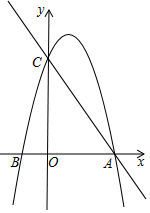
如图，直线y=-$\frac{4}{3}$x+4与x轴交于点A，与y轴交于点C，已知二次函数的图象经过点A、C和点B（-1，0）．