题目内容
16. 如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(-4,8),对角线AC⊥x轴于点C,点D在y轴上,求直线AB的解析式.
如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(-4,8),对角线AC⊥x轴于点C,点D在y轴上,求直线AB的解析式.
分析 根据正方形的性质求出点B的坐标,即可用待定系数法求出直线AB解析式.
解答  解:连接BD,过B点作BE⊥x轴,E为垂足,
解:连接BD,过B点作BE⊥x轴,E为垂足,
由已知得AC=BD=8,
BE=$\frac{1}{2}$AC=4,
故B点坐标为(-8,4),
设直线AB的解析式为y=kx+b,则
$\left\{\begin{array}{l}{-8k+b=4}\\{-4k+b=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=12}\end{array}\right.$.
故直线AB的解析式为y=x+12.
点评 本题考查正方形的性质、待定系数法确定函数解析式,解题的关键是确定B点坐标,需要熟练掌握待定系数法求函数解析式,属于中考常考题型.

练习册系列答案
相关题目
2.大运河森林公园位于北京市通州区的北运河两侧,占地面积约为10700亩,公园沿水系长达8公里,分别建有潞河桃柳、月岛闻莺、明镜移舟等六大景区和长虹花雨、半山人家、皇木古渡等十八处景点.将10700用科学记数法表示应为( )
| A. | 1.07×104 | B. | 10.7×103 | C. | 1.07×105 | D. | 0.107×105 |
4.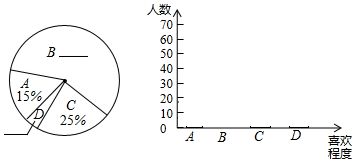 某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
请你根据以上提供的信息,解答下列问题:
(1)补全上面的频数分布表和扇形统计图;
(2)根据补全的频数分布表画出频数分布直方图;
(3)若该校七年级共有600名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
 某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表. | 喜欢程度 | 频数 |
| A | 18 |
| B | 66 |
| C | 30 |
| D | 6 |
(1)补全上面的频数分布表和扇形统计图;
(2)根据补全的频数分布表画出频数分布直方图;
(3)若该校七年级共有600名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
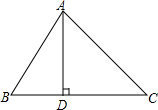 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.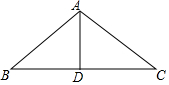 如图,在△ABC中,AB=5cm,BC=8cm,BC边上的中线AD=3cm,求∠ADC的度数.
如图,在△ABC中,AB=5cm,BC=8cm,BC边上的中线AD=3cm,求∠ADC的度数.
 如图,一次函数y=kx+6的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(x<0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,且OB:OA:OD=6:3:2
如图,一次函数y=kx+6的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(x<0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,且OB:OA:OD=6:3:2