题目内容
19. 如图,菱形ABCD的边长为4,∠ABC=120°.点E是AB边上的动点,点F是对角线AC上的动点,则EF+BF的最小值为2$\sqrt{3}$.
如图,菱形ABCD的边长为4,∠ABC=120°.点E是AB边上的动点,点F是对角线AC上的动点,则EF+BF的最小值为2$\sqrt{3}$.
分析 过点D作DE⊥AB于E,交AC于点F,连接BF,则DE的长即为EF+BF的最小值,根据菱形ABCD中∠ABC=120°求得∠BAD的度数,进而判断出△ADE是含30°角的直角三角形,根据勾股定理即可得出DE的长.
解答 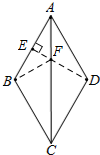 解:过点D作DE⊥AB于E,交AC于点F,连接BF,则BF=DF,
解:过点D作DE⊥AB于E,交AC于点F,连接BF,则BF=DF,
∴EF+BF=EF+DF=DE(最短),
∵∠ABC=120°,
∴∠DAE=60°,
∴∠ADE=30°,
∵菱形ABCD的边长为4,
∴AE=$\frac{1}{2}$AD=2,
∴Rt△ADE中,DE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$
点评 本题以最短距离问题为背景,主要考查了菱形的性质以及轴对称的性质.最短距离问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{6}-\sqrt{3}=\sqrt{3}$ | B. | $\sqrt{6}÷\sqrt{3}=\sqrt{2}$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{9}=±3$ |
9.一个多边形的内角和比外角和的3倍多180度,那么这个多边形的边数是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
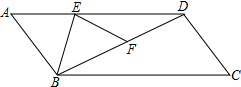 E为?ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=51°.
E为?ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=51°. 如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是6.
如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是6. 如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.
如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于E.