题目内容
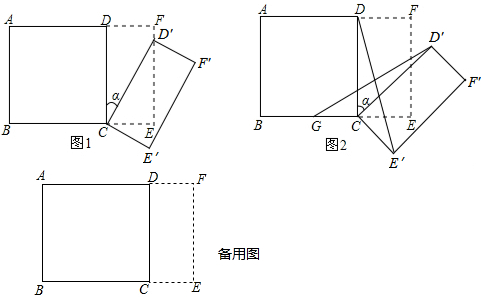
13.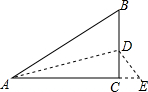 如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 由有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,利用勾股定理即可求得AB的长,然后由折叠的性质,求得AE的长,继而求得答案.
解答 解:∵∠C=90°,AC=2,BC=$\frac{3}{2}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{5}{2}$,
由折叠的性质可得:AE=AB=$\frac{5}{2}$,
∴CE=AE-AC=$\frac{1}{2}$.
故选A.
点评 此题考查了折叠的性质以及勾股定理.注意掌握折叠前后图形的对应关系是解此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.在某校举行的“汉字听写”大赛中,七名学生听写汉字的个数分别为350,310,320,250,310,340,360,则这组数据的中位数是( )
| A. | 330 | B. | 320 | C. | 310 | D. | 250 |
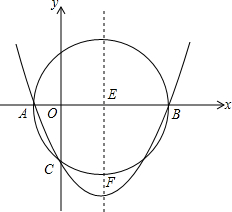 如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.
如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.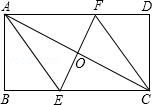 如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.
如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.