题目内容
3.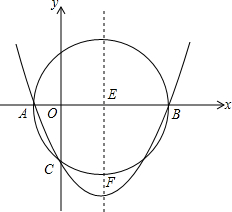 如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.
如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.(1)求抛物线的解析式及顶点F的坐标.
(2)已知M为抛物线上一动点(不与C点重合)试探究:使得以A、B、M为顶点的三解形面积与△ABC的面积相等.求所有符合条件的点M的坐标.
分析 (1)首先连接CE,由以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,可求得A,B的坐标,然后由勾股定理求得OC的长,即求得点C的坐标,然后利用交点式,求得抛物线的解析式,继而求得顶点F的坐标.
(2)由以A、B、M为顶点的三解形面积与△ABC的面积相等,可求得点M的纵坐标为±4,继而求得答案.
解答  解:(1)连接CE,
解:(1)连接CE,
∵以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,
∴OE=3,AE=BE=5,AE=BE=CE=5,
∴OA=AE-OE=2,OB=OE+BE=8,
∴A(-2,0),B(8,0),
在Rt△COE中,OC=$\sqrt{C{E}^{2}-O{E}^{2}}$=4,
∴点C的坐标为:(0,-4),
设抛物线的解析式为:y=a(x+2)(x-8),
把点C(0,-4)代入得:-16a=-4,
解得:a=$\frac{1}{4}$,
∴抛物线的解析式为:y=$\frac{1}{4}$(x+2)(x-8)=$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{1}{4}$(x-3)2-$\frac{25}{4}$,
∴顶点F的坐标为:(3,-$\frac{25}{4}$);
(2)解:∵S△ABC=$\frac{1}{2}$AB•OC,S△ABM=$\frac{1}{2}$AB•|yM|,S△ABC=S△ABM,
∴|yM|=4,
即yM=±4,
若yM=-4时,$\frac{1}{4}$(x-3)2-$\frac{25}{4}$=-4,解得:xM=0或6,
又∵xM≠0,
∴M(6,-4);
若yM=4时,$\frac{1}{4}$(x-3)2-$\frac{25}{4}$=4,解得:xM=3±$\sqrt{41}$,
即M(3+$\sqrt{41}$,4)或M(3-$\sqrt{41}$,4),
综上所述,M点的坐标为(6,-4)或(3+$\sqrt{41}$,4)或(3-$\sqrt{41}$,4).
点评 此题属于圆的综合题.考查了待定系数求二次函数解析式、垂径定理以及三角形面积问题.注意准确作出辅助线,求得点C的坐标是解此题的关键.

| A. | -3 | B. | 0 | C. | 3 | D. | 6 |
| A. | 1.6×104 | B. | 0.16×10-3 | C. | 1.6×10-4 | D. | 16×10-5 |
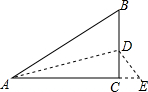 如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=$\frac{3}{2}$,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |